Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 46

Duas cargas puntiformes positivas, com carga Q , estão no eixo y , uma em y = + a e outra em y = - a . (a) Mostre que a intensidade do campo elétrico no eixo x é máxima em x = a / 2 e em x = - a / 2 , calculando ∂ E x / ∂ x e igualando a derivada a zero. (b) Represente graficamente a função E x versus x usando os resultados da parte (a) deste problema e levando em consideração que E x é aproximadamente igual a 2 k q x / a 3 quando x é muito menor do que a e E x é aproximadamente igual a 2 k q / x 2 quando x é muito maior que a .

Passo 1

Nesse exercício, vamos utilizar o resultado já obtido no exercício 44 (não deixe de ver a nossa resolução caso sinta alguma dificuldade :D). Lá, descobrimos que o campo elétrico no eixo x era dado por:

E x = 2 k q x x 2 + a 2 3 / 2

Passo 2

  1. Vamos derivar a expressão acima em relação a x :

    2. ∂ E x ∂ x = ∂ ∂ x 2 k q x x 2 + a 2 3 / 2 ∂ E x ∂ x = 2 k q ∂ ∂ x x x 2 + a 2 3 / 2 ∂ E x ∂ x = 2 k q ⋅ x 2 + a 2 3 / 2 - x ⋅ 2 x ⋅ 3 2 ⋅ x 2 + a 2 1 / 2 x 2 + a 2 ∂ E x ∂ x = 2 k q ⋅ x 2 + a 2 1 / 2 x 2 + a 2 - 3 x 2 x 2 + a 2 = 2 k q ⋅ a 2 - 2 x 2 x 2 + a 2 1 / 2  

    Assim, para encontramos o valor máximo, bastará fazer

    ∂ E x ∂ x = 0 ⟹ a 2 - 2 x 2 = 0 ∴ x = ± a 2

    Passo 3

  2. Temos o seguinte

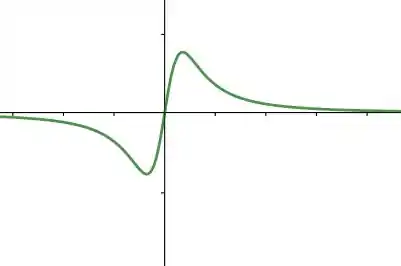
Veja que, realmente obtemos valores máximos de E para dois pontos!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elétron se encontra no vácuo, perto da superfície da Terra, no ponto y = 0 de um eixo vertical. Qual deve ser a coordenada y de um segundo elétron situado no eixo y para que a força eletrostática e
Duas cargas pontuais de 30n C e - 40n C são mantidas fixas no eixo x , na origem e no ponto x = 72c m , respectivamente. Uma partícula com uma carga de 42μ C é liberada a partir do repouso no ponto x
No decaimento radioativo da Eq. abaixo, um núcleo de U 238 se transforma em T h 234 e H e 4 , que é ejetado. (Trata-se de núcleos e não de átomos; assim, não há elétrons envolvidos.) Para uma distânci
Na Fig 21 - 4 4 , determine ( a ) o módulo e ( b ) a orientação da força eletrostática total a que está submetida a partícula 4 . Todas as partículas são mantidas fixas no plano x y ; q 1 = - 3.2 × 10
Três partículas carregadas formam um triângulo: a partícula 1, com uma carga Q 1 = 80,0 nC, está no ponto (0; 3,00 mm) ; a partícula 2, com uma carga Q 2 , está no ponto (O; -3,00 mm) e a partícula 3,