Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.4 - Ex. 26

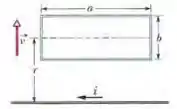
Na Fig. 30-54, uma espira retangular de comprimento a = 2,2   c m , largura b = 0,80   c m e resistência R = 0,40   m Ω é colocada nas vizinhanças de um fio infinitamente longo percorrido por uma corrente i = 4,7   A . Em seguida, a espira é afastada do fio com uma velocidade constante v = 3,2   m m / s . Quando o centro da espira está a uma distância r = 1,5 b do fio, determine (a) o valor absoluto do fluxo magnético que atravessa a espira e (b) a corrente induzida na espira.

Passo 1

E aí, galera! 😉

O problema tem uma espira retangular se afastando com velocidade v = d r / d t de um fio pelo qual passa uma corrente i . O campo produzido pelo fio sobre a espira é para dentro da folha, de modo que o fluxo será negativo (estamos adotando a normal para fora da folha).

Para uma faixa horizontal fininha de espessura d r e largura a a uma distância r do fio, o fluxo ser��

d Φ B = - B   d A = - B   a   d r = - μ 0 i 2 π r a   d r

Veja só! 😎

Passo 2

Na última passagem usei a fórmula do campo do fio infinito. Agora basta integra r de r - b / 2 até r + b / 2 :

Φ B = - μ 0 i a 2 π ∫ r - b 2 r + b 2 1 r   d r = - μ 0 i a 2 π ln ⁡ r + b 2 r - b 2 = - μ 0 i a 2 π ln ⁡ 2 r + b 2 r - b

Usando r = 1,5 b , temos

ϕ B = - μ 0 i a 2 π ln ⁡ 4 b 2 b = - μ 0 i a 2 π ln ⁡ 2

Com a = 0,022   m e i = 4,7   A :

Φ B = 1,4 ⋅ 10 - 8   W b

Tranquilo até aqui? 😬

Passo 3

Agora precisamos achar a corrente induzida na espira. Para isso, o primeiro passo é achar a fem, dada pela lei de Faraday:

ε = - d Φ B d t

Cuidado aqui: você não pode fazer r = 1,5 b antes de derivar: primeiro derive e depois faz a substituição!

Assim,

ε = μ 0 i a 2 π ⋅ 1 r + b 2 r - b 2 ⋅ r + b 2 r - b 2 ' = μ 0 i a 2 π ⋅ r - b 2 r + b 2 ⋅ r - b 2 - r + b 2 r - b 2 2 ⋅ d r d t

Portanto,

ε = - 2 μ 0 i a b π   2 r + b ( 2 r - b ) ⋅ d r d t

Vimos também que

d r d t = v

Logo,

ε = - 2 μ 0 i a b v π   2 r + b ( 2 r - b )

Está acompanhando? 😐

Passo 4

Para achar a corrente, recorremos à lei de Ohm:

ε = R i i n d ⇒ i i n d = ε R = - 2 μ 0 i a b v π   2 r + b ( 2 r - b ) R

Fazendo r = 1,5 b :

i i n d = - μ 0 i a v 4 π b R

Substituindo i = 4,7   A , a = 0,022   m , b = 0,0080   c m , v = 3,2 ⋅ 10 - 3   m / s e R = 0,40 ⋅ 10 - 3 Ω :

i i n d = 1,0 ⋅ 10 - 5 A

Como i i n d < 0 , a corrente induzida está no sentido horário.

E aí! Entendeu tudo? Responde Aí! 😁

Resposta

Φ B = 1,4 ⋅ 10 - 8   W b

i i n d = 1,0 ⋅ 10 - 5 A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um material condutor elástico é esticado e usado para fazer uma espira circular com 12,0c m de raio, que é submetida a um campo magnético uniforme de 0,800T perpendicular ao plano da espira. Ao ser li
Na figura 30-36, o fluxo do campo amgnético na espira aumenta de aordo com a equação ϕ B = 6,0 t 2 + 7,0 t , onde ϕ B está em miliwebers e t em segundos. (a) Qual é o módulo da força eletromotri induz
Uma espira com 12c m de raio e uma resistência de 8,5o h m s é submetida a um campo magnético uniforme B → cujo módulo varia de acorco com a figura 30-33. A escala do eixo vertical é definida por B S
Na figura 30-39, uma bobina de 120 espiras, com 1,8c m de raio e uma resistência de 5,3o h m s , é coaxial com um solenoide de 220e s p i r a s / c m e 3,2c m de diâmetro. A corrente no solenoide dimi
Uma pequena espira com 6,8m m 2 de área é colocada no interior de um solenoide longo com 854e s p i r a s / c m , percorrido por uma corrente senoidal i com 1,28A de amplitude e uma frequência angular