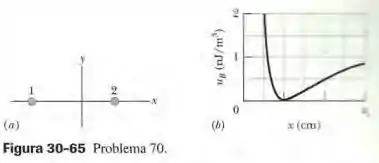
A Fig. 30-65ª mostra, em seção reta, dois fios retilíneos, paralelos e muito compridos. A razão entre a corrente no fio 1 e a corrente no fio 2 é . O fio 1 é mantido fixo no lugar. O fio 2 pode ser deslocado ao longo do semieixo positivo, o que faz variar a densidade de energia magnética criada pelas duas correntes na origem. A Fig. 30-65b mostra um gráfico de em função da posição do fio 2. A curva tem uma assíntota para e a escala do eixo horizontal é definida por . Determine os valores de (a) e (b) .

Temos dois fios posicionados no eixo . O fio 1 é mantido fixo enquanto o 2 pode ser movido. Estamos interessados em ver o que acontece com a densidade de energia (portanto o campo magnético) na origem (): essa densidade é mostrada no gráfico.

Como o fio está parado, sua contribuição para o campo é sempre a mesma. Desta forma, vamos tentar calcular o seu campo primeiro. Para isso, note quando o fio 2 é posicionado em , o campo resultante na origem é nulo. Assim, podemos dizer que os campos dos fios 1 e 2 se anulam:

denota a distância do fio 1 à origem e neste caso, que representa o caso em que a densidade de energia (e consequentemente o campo resultante) é nulo na origem. Desta forma, achamos que