Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.10 - Ex. 44
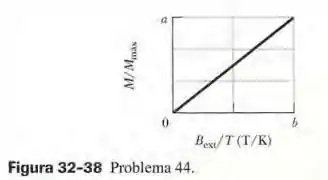
A Fig. 32-28 mostra a curva de magnetização de um material paramagnético. A escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . Seja o valor experimental do momento magnético de uma amostra e o valor máximo possível da mesma amostra. De acordo com a lei de Curie, qual é o valor da razão quando a amostra é submetida a um campo magnético de a uma temperatura de ?
Passo 1
A questão diz que uma certa amostra satisfaz a lei de Curie e pede para calcularmos a razão para e . Do gráfico dado, tiramos que
Por outro lado, como se trata de uma mesma amostra, a razão das magnetizações deve ser igual a razão dos momentos magnéticos:
Passo 2
Assim, usando , , e :
Portanto,
Resposta
Exercícios de Livros Relacionados
Um anel de Rowland é feito de um material ferromagnético. O anel tem seção reta circular, com um raio interno de 5,0c m e um raio externo de 6,0c m , e uma bobina primária enrolada no anel possui 400
O módulo do momento dipolar associado a um átomo de ferro em uma barra de ferro é 2,1 ⋅ 10 - 23J / T . Suponha que os momentos dipolares de todos os átomos da barra, que tem 5,0c m de comprimento e um
Uma bússola é colocada em uma superfície horizontal e a agulha recebe um leve empurrão que a faz oscilar em torno da posição de equilíbrio. A frequência de oscilação é de 0,312H z . O campo magnético
A Terra possui um momento dipolar magnético de 8,0 ⋅ 10 22J / T . (a) Se esse momento dipolar fosse causado por uma esfera de ferro magnetizada situada no centro da Terra, qual deveria ser o raio da e
Uma onda eletromagnetica com intensidade igual a 200 x W/mi é normal a um cartio preto retangular de 20 cm por 30 cm que absorve 100 por cento da onda.Determine a forca exercida no cartlo pela radiaco