Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.4 - Ex. 22
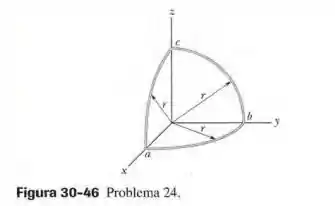
Uma espira é formada por três segmentos circulares, todos de raio , como mostra a Fig. 30-46. Cada segmento é um quarto de circunferência: está no plano , no plano e no plano . (a) Se um campo magnético uniforme aponta no sentido positivo do eixo , qual é o valor absoluto da força eletromotriz que aparece na espira quando aumenta à taxa de ? (b) Qual é o sentido da corrente no segmento ?
Passo 1
A questão fornece uma espira tridimensional formada por três segmentos circulares, limitando três regiões planas. Como o campo magnético é paralela ao eixo , apenas a superfícies no plano deve ser considerada para o cálculo do fluxo:
As outras áreas planas nos demais planos tem fluxo nulo pois o campo é perpendicular às normais.
Passo 2
Para calcular a fem induzida, basta usar a lei de Faraday:
Como é constante e varia no tempo:
Como é dito que o campo está aumentando, temos que
Assim,
Como queremos o módulo:
Assim,
Passo 3
Vimos no passo anterior que , de modo que a corrente percorrerá a espira no sentido contrário a convenção. Como a normal foi convencionada na direção positiva do eixo , o sentido positivo da corrente é o sentido horário (de para ).
Desta forma, a corrente deve percorrer a espira de para .