Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.4 - Ex. 24
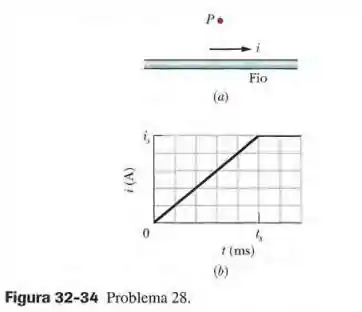
A Fig. 32-34a mostra a corrente que atravessa um fio de resistividade . O módulo da corrente em função do tempo está plotado na Fig. 32-34b. A escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . O ponto está a uma distância radial de do centro do fio. Determine o módulo do campo magnético no ponto devido à corrente (a) em , (b) em , (c) em . Suponha agora que o campo elétrico responsável pela corrente existe apenas no interior do fio e determine o módulo do campo magnético no ponto devido à corrente de deslocamento no fio (d) em , (e) em e (f) em . No ponto em , determine o sentido (para dentro ou para fora do papel) (g) de ; (h) .
Passo 1
Nos três primeiros itens devemos calcular o campo magnético produzido por um fio longo em um ponto a uma distância do fio. Sabemos que o campo é dado por
Em , tiramos do gráfico que . Assim, o campo será
Já em , vemos que , de modo que
Por fim, em , . Portanto,
Passo 2
Para os itens (d), (e) e (f) temos que ter o seguinte raciocínio: como a corrente varia no tempo, ela vai induzir uma corrente de deslocamento
Mas como , temos que
Como :
O campo magnético gerado por essa corrente de deslocamento no ponto será:
Vamos usar e . Tanto para quanto para , temos que
Assim, em ambos os instantes:
Agora, para o item (f), note que em a corrente não varia, isto é
Assim,
Passo 3
Nos dois casos, o sentido do campo é para fora do papel. Para , vemos que a corrente aponta para a direita, de modo que pela regra da mão, o campo deve sair do papel no ponto .
Já para , como , a corrente de deslocamento tem o mesmo sentido de , de modo que o campo gerado também deve ter o mesmo sentido.
Resposta
Para fora do papel
Para fora do papel