Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.4 - Ex. 21
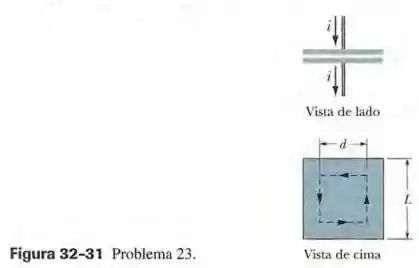
Na Fig. 32-31, um capacitor de placas paralelas possui placas quadradas de lado . Uma corrente de carrega o capacitor, produzindo um campo elétrico uniforme entre as placas com perpendicular às placas. (a) Determine a corrente de deslocamento na região entre as placas. (b) Determine o valor de nessa região. (c) Determine a corrente de deslocamento envolvida pela trajetória tracejada, um quadrado com de lado. (d) Determine o valor de ao longo da trajetória tracejada.
Passo 1
O problema fala de um capacitor de placas quadradas alimentado por uma corrente . É óbvio que entre as placas do capacitor não existe uma corrente de cargas passando. Mas devido à correção de Maxwell na lei de Ampère, podemos interpretar a variação do fluxo elétrico entre as placas como uma corrente de deslocamento:
Essa corrente “fictícia” tem o mesmo valor da corrente que passa no fio e alimenta o capacitor. É como se essa corrente fictícia entre as placas mantivesse um fluxo de carga contínuo no circuito. Assim, temos que
Passo 2
O fluxo elétrico entre as placas é dado por
Assim,
Portanto,
Substituindo e :
Passo 3
A corrente de deslocamento que passa pelo quadrado de lado será proporcional a área desse quadrado. Podemos fazer a seguinte proporção:
Assim,
Portanto,
Passo 4
Por fim, temos que calcular sobre o quadrado de lado . Para isso, basta lembrar que
Como , temos que