Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.4 - Ex. 29
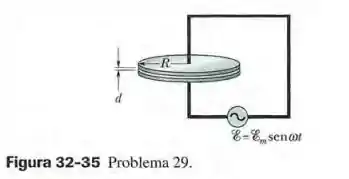
Na Fig. 32-35, um capacitor de placas circulares de raio está ligado a uma fonte de força eletromotriz , onde e . O valor máximo da corrente de deslocamento é . Despreze o efeito de borda. (a) Qual é o valor máximo da corrente no circuito? (b) Qual é o valor máximo de , onde é o fluxo elétrico através da região entre as placas? (c) Qual é a distância entre as placas? (d) Determine o valor máximo do módulo de entre as placas a uma distância do centro.
Passo 1
O problema fala de um capacitor ligado a um gerador de corrente alternada. No item (a) ele pergunta qual é o valor máximo da corrente no circuito, sabendo que o valor máximo da corrente de deslocamento entre as placas do capacitor é .
Sabemos que a corrente de deslocamento em um capacitor é igual a corrente que o alimenta pelo circuito. Assim,
Portanto,
Passo 2
No item (b) devemos calcular o valor máximo da taxa de variação do fluxo elétrico. Sabemos que a corrente de deslocamento é dada por
Usando , tiramos que o valor máximo da variação do fluxo é
Passo 3
Agora queremos achar a distância entre as placas. Para isso, lembre-se que
Mas entre as placas do capacitor o campo é uniforme, de modo que
Assim,
Mas como , temos que
Assim,
Como temos informações sobre os valores máximos, vamos tomar . Assim,
Substituindo os valores:
Passo 4
Queremos o campo magnético induzido pela corrente de deslocamento a uma distância . Pela lei de Ampère:
Neste caso, temos que fazer uma proporção para achar em função de , já que representa a corrente pela placa toda e apenas pelo círculo de raio . Assim,
Assim,
Portanto, da lei de Ampère:
Substituindo os dados com :