Enunciado
Física - Halliday - Vol 4- Ed: 9º - Capítulo 33.6 - Ex. 26
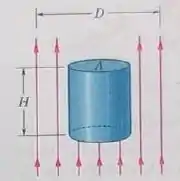
Na Fig. 33-38, o feixe de um laser com de potência e de diâmetro é apontado para cima, perpendicularmente a uma das faces circulares (com menos de de diâmetro) de um cilindro perfeitamente refletor, que é mantido suspenso pela pressão da radiação do laser. A massa específica do cilindro é . Qual é a altura H do cilindro?
Passo 1
Os dados que o problema nos trás são:
E sabemos que massa é densidade vezes volume, e o volume do cilindro pode ser escrito como a mutiplicação da área da base pela altura :
Passo 2
Como há equilíbrio das forças, temos que a força de radiação equilibra a força peso:
Mas não temos a intensidade, mas sim a potência e a posição , então a altura do cilindro fica:
Passo 3
Agora é só substituir! Bora fazer?
Resposta
Exercícios de Livros Relacionados
Quando um cometa se aproxima do Sol, o gelo da superfície do cometa sublima, liberando íons e partículas de poeira. Como os íons possuem carga elétrica, são empurrados pelas partículas carregadas do v
No sistema solar, uma partícula está sujeita a influência combinada da atração gravitacional do Sol e da força da radiação solar. Suponha que a partícula é uma esfera com uma massa especifica de 1,0 ⋅
Em uma região do espaço onde as forças gravitacionais podem ser desprezadas, uma esfera é aceleradapor um feixe luminoso uniforme de intensidade 6,0n W / m 2 . A esfera, totalmente absorvente tem um r
Um feixe de 20kW de radiacao eletromagnetica enormal a uma superficie que reflete 50 por cento da radiacao.Qual a forca exercida pela radiacao na superficie?
Pequenas particulas são sopradas pelo sistema solar pela pressão de radiação da luz do Sol. Considere que cada particula seja esférica de raio r, massa especifica de 1,00 g/cm\' e absorva toda a radia