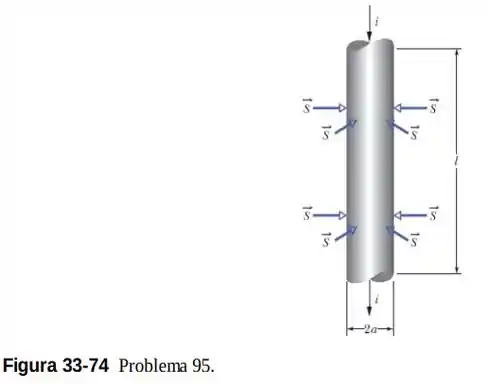
A Fig. 33-74 mostra um resistor cilíndrico de comprimento , raio e resistividade , que conduz uma corrente . (a) Mostre que o vetor de Poynting na superfície do resistor é perpendicular à superfície, como indicado na figura. (b) Mostre também que a taxa com a qual a energia penetra no resistor através da superfície cilíndrica, calculada integrando o vetor de Poynting ao longo da superfície, é a taxa de produção de energia térmica:

em que é um elemento de área da superfície cilíndrica e é a resistência do resistor

a) Pois muito bem! Vamos começar, então!

Nesse primeiro item, a questão pede pra gente mostrar que o vetor de Poynting na superfície do resistor é perpendicular à superfície.

A questão fornece pra gente na imagem da figura do enunciado a corrente circulando no fio cilíndrico, de baixo para cima. Vamos começar nosso raciocínio, considerando que o cilindro coinicide com um dos nossos eixos de referência, que é o eixo . E nesse caso, o semieixo positivo vai apontar pra cima.

Analisando a forma como a corrente está circulando, temos que o campo magnético vai apontar no sentido horário concentricamente à seção transversal do fio.

E uma vez que adotamos que o eixo coincide com o resistor e aponta para cima, tanto a corrente como o campo elétrico apontam no sentido do semieixo negativo.

Então, dado que o vetor nada mais é do que o produto vetorial entre os vetores campo elétrico e campo magnético, basta usar um truquezinho que o produtor vai te passar!

Vamos determinar a orientação de com base em versores. Versores são os vetores unitários, que tem a mesma orientação que um eixo. No nosso caso, os versores correspondente são , e ; equivalentes respectivamente às direções perpendicular, radial e transversal ao eixo.

Se liga só! O vetor campo elétrico tem orientação no sentido negativo do eixo . Então, o versor correspondente é . Já o vetor campo magnético aponta no sentido horário. Por convenção, costumamos adotar o sentido horário como negativo. Desse modo, temos que o versor correspondente é .

Como , então aponta na direção de...

Ou seja, temos a comprovação de que aponta radialmente para dentro do resistor.

b) Para esse segundo item,temos que determinar a taxa com a qual a energia penetra no resistor através da superfície cilíndrica, que é calculada integrando o vetor de Poynting ao longo da superfície.

Bom! Primeiro tem que se ligar no módulo do vetor de Poynting, né? Que é dado pela seguinte fórmula...

Precisamos do módulo dos vetores e !

Pois muito bem! Como esse problema é similar ao anterior, onde também tínhamos um fio cilíndrico resistor percorrido por corrente, as fórmulas para obter e são praticamente as mesmas. No nosso caso, elas são dadas por...

Sendo assim, temos que...

Onde como o módulo do vetor de Poynting é constante, temos então que...

E como é referente apenas à área de superfície cilíndrica, ou seja a área lateral, ignoraremos a seção transversal. Desse modo...

Chegando assim, ao resultado desejado!

Good work, guys!