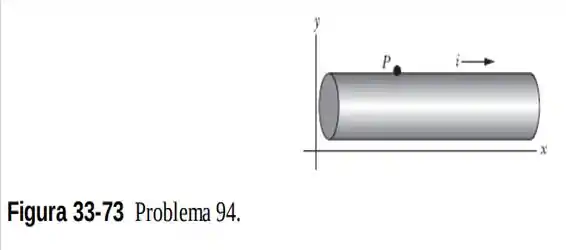
Na Fig. 33-73, um fio longo e retilíneo, com de diâmetro e uma resistência de por , conduz uma corrente uniforme de no sentido positivo do eixo . Calcule, para um ponto P na superfície do fio, (a) o módulo do campo elétrico , (b) o módulo do campo magnético e (c) o módulo do vetor de Poynting. (d) Determine a orientação de .

a) Pois muito bem! Vamos começar, então!

Nesse primeiro item, a questão pede pra gente calcular o módulo do campo elétrico naquele ponto P destacado na figura do enunciado.

A questão fornece pra gente a corrente circulando no fio cilíndrico, o comprimento do fio (que chamaremos de ), sua resistência () e seu raio .

Uma vez que está circulando no fio uma corrente, é devido ao fato de que uma diferença de potencial está sendo gerada. E essa diferença de potencial, que chamaremos de , pode ser dada em função da resistência e da corrente por...

Agora se liga só! Todos os pontos na superfície do rio, estão sujeitos ao mesmo campo elétrico. E com base nesse potencial elétrico que a gente acabou de descobrir, podemos relacioná-lo com um dado que a gente tem, que é o comprimento ... Sendo assim, temos que:

Calculando, obtemos o nosso valor...

Onde o campo elétrico no ponto aponta no mesmo sentido que a corrente, ou seja, no sentido do semieixo positivo.

b) Para esse segundo item, temos que obter o módulo do campo magnético em !

Dos estudos sobre magnetismo, sabemos que quando um fio retilíneo é percorrido com uma corrente elétrica , ele gera ao seu redor um campo magnético, cujas as linhas do campo são circunferências concêntricas pertencentes ao plano perpendicular ao fio e com centro comum em um ponto dele.

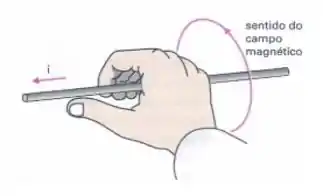
E através da lei de Ampére conseguimos determinar o módulo do campo magnético. Ela nos diz que “o vetor campo magnético é tangente as linhas do campo magnético”. Assim a tangente as linhas do campo magnética será a direção dele, e a intensidade do campo será dado pela seguinte equação:

Onde é a constante de permeabilidade magnética do meio (no caso o vácuo), e igual a ... Sendo assim, temos que:

E esse campo, como já comentamos brevemente, aponta no sentido do semieixo positivo (para fora do papel).

c) Quando ao módulo do vetor de Poynting, , com base em nossa bibliografia, temos que ele é dado por...

E dado que já sabemos e , então podemos determinar como:

d) Por fim, falta determinar a orientação de .

Sabemos que o vetor campo elétrico aponta na direção do semieixo positivo e o campo magnético aponta na direção do semieixo positivo.

Com isso, usando a regra da mão direita, podemos constatar que o que o vetor de Poynting no ponto aponta no sentido do semieixo negativo.

Outra forma de resolver esse item é usando versores. Versores são vetores unitários que apresentam a mesma orientação de um eixo.

No caso dos eixos e ; os versores correspondentes respectivamente são , e .

Agora, repara na tabela abaixo que mostra o produto vetorial desses versores...

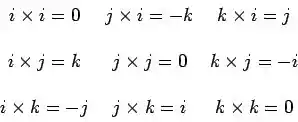
A gente sabe que ! Ou seja, temos na mão nada mais do que o produto vetorial entre o versor (no eixo ) com o versor (do eixo ). E pela imagem acima, podemos ver que isso nos resulta em um versor , nos dando um vetor que aponta para o semieixo negativo.

Entendeu a sacada?

Bora pra frente que atrás vem gente!