Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.1 - Ex. 3
Uma fonte luminosa e isotrópica S é posicionada a uma distância de uma tela de observação e a intensidade luminosa no ponto (na mesma altura que S) é medida. Em seguida um espelho plano é colocado atrás de S a uma distância . De quantas vezes aumenta a intensidade luminosa quando o espelho é intruduzido.
Passo 1
Antes de começar a resolver, vamos esquematizar com um desenho a situação colocada pelo enunciado.
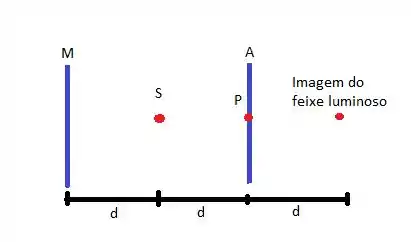
A intensidade luminosa pode ser calculada a partir da relação:
Onde:
Isso porque a potência para este caso não mudará em nenhum momento.
Passo 2
A intensidade total é:
Onde é a intensidade no ponto P e é a intensidade no espelho M.
Desta forma podemos calcular as intensidades.
Temos que para é pois após a luz chegar no espelho ela e refletida e parece ser produzida pela imagem do feixe luminoso que está a uma distância do espelho M.
Passo 3
Calculando a intensidade total:
Desta forma ao intruduzir o espelho a intensidade aumenta:
Resposta
A intensidade aumenta 1,11.