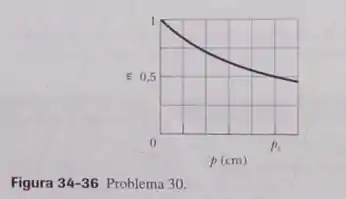
A Fig. 34-36 mostra a ampliação lateral em função da distância entre um objeto e um espelho esférico quando o objeto é deslocado ao longo do eixo central do espelho. A escala do eixo horizontal é definida por . Qual é a ampliação do objeto quando se encontra a do espelho?

Bom, como a gente pode ver no gráfico, de zero até têm cinco retângulos, como vale , cada retângulo vale , além disso exatamente em , .

Mas se substituirmos na equação da ampliação:

Para obtermos , não poderemos usar o mesmo valor para quando porque varia junto com .

Vamos então usar a equação de espelhos esféricos:

E isolar :

Para substituir ele na equação da ampliação: