Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.2 - Ex. 24
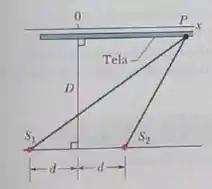
Na Fig. 35-38, duas fontes pontuais isotrópicas, e , emitem luz em fase com comprimento de onda e a mesma ainplitude. As fontes, separadas por uma distância , estão em uma reta paralela ao eixo . O eixo está em uma tela de observação situada a uma distância das fontes, com a origem equidistante das fontes. A figura mostra dois raios que chegam ao mesmo ponto da tela, situado a uma distância da origem.
(a) Para que valor de raios apresentam a menor diferença de fase possível?
(b) Para que múltiplo de a diferença de fase é a menor possível?
(c) Para que valor de os raios apresentam a maior diferença de fase possível?
(d) Para que múltiplo de a diferença de fase é a maior possível?
(e) Qual é a diferença de fase para ?
(f) Para , a intensidade da luz no ponto é máxima, mínima, mais proxima de máxima ou mais próxima de mínima?
Passo 1
Letra a)
Sabemos que no experimento da fenda dupla, o máximo representa um ponto claro na tela e temos diferença de fase zero. E para isso acontecer, olhando a simetria da figura, o valor de deve ser , bem no centro das duas fontes.
Passo 2
Letra b)
Conforme vimos no passo anterior, a diferença de fase é menor possível quando temos .
Passo 3
Letra c)
A tela se estende até o infinito, certo? E a maior diferença de fase seria exatamente na borda da tela, que é quando temos a maior diferença entre as fases. Bom, como infinito não é um número, não podemos dizer quanto exatamente será isso, só nos basta dizer que a maior diferença de fase será quando .
Passo 4
Letra d)
Agora vamos pensar um pouco sobre os comprimentos de onda. A maior diferença de fase seria quando , certo? Então podemos considerar que os raios chegam praticamente paralelos e horizontais na tela. E considerando isso, a diferença de percurso vai ser somente a separação entre as fontes (olha lá na figura e vê se não é )!
Mas saca só o que o enunciado nos diz: “As fontes, separadas por uma distância ”, então daqui podemos tirar a distância de separação em função de
É isso aí! O múltiplo de para a diferença de fase máxima é !
Passo 5
Letra e)
A diferença de fase é dada pela diferença entre os caminhos percorridos pelas ondas, certo?
Certo?
Bom, aqui vamos ter de olhar com mais carinho para o desenho:
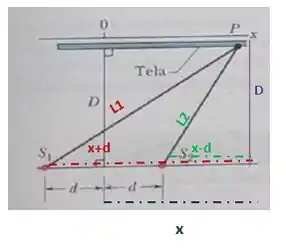
Por Pitágoras podemos formar dois triângulos ali em cima: um usando o caminho e os catetos e e o outro é usando o caminho e os catetos e . Daí os caminhos ficam em termos da distância :
E sabemos que e que e , então agora é só substituir para determinar a diferença de fase :
Agora cortando os dos dois lados e calculando as raízes temos:
Passo 6
Letra f)
A interferência destrutiva mais próxima seria com enquanto que a interferência construtiva seria com . Como encontramos uma diferença de fase de e está mais próxima de do que de , a intensidade é mais próxima de mínima do que de máxima =)