Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.4 - Ex. 75
A Fig. 35-45a mostra uma lente com raio de curvatura pousada em uma placa de vidro e iluminada por cima por uma luz de comprimento de onda . A Fig. 35-45b (uma fotografia tirada de um ponto acima da lente) revela a existência de franjas de interferência circulares (os chamados anéis de Newton) associadas à espessura variável do filme de ar que existe entre a lente e a placa. Determine os raios dos anéis que correspondem aos máximos de interferência, supondo .
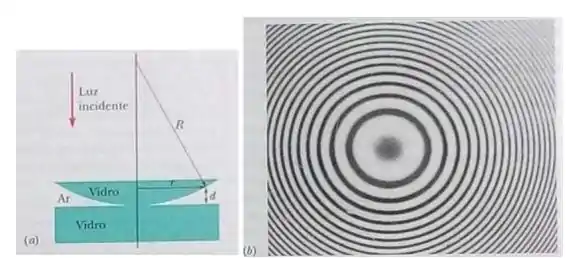
Passo 1
A questão pede para encontrarmos os raios dos anéis claros, que correspondem aos máximo de interferência! Para isso, temos que considerar a camada de ar entre a lente e a placa como um filme fino de espessura variável.
Quando a reflexão ocorre do vidro para o ar não há mudança de fase, mas do ar para o vidro sim. Desta forma, temos que adicionar na defasagem:
A diferença de caminho será onde é a espessura do filme de ar:
Passo 2
Agora vem a parte que temos que usar geometria:
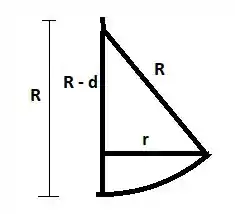
Aplicando o teorema de Pitágoras:
Assim,
Aqui vamos usar a aproximação dada que :
Para , vale . Assim,
Portanto,
Logo,
Passo 3
Como queremos os pontos de interferência construtiva (franjas claras):
Assim,
Portanto,
Se quiséssemos achar as franjas escuras: