Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.4 - Ex. 78
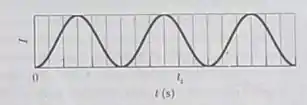
Um filme fino de um líquido é mantido em um disco horizontal, com ar dos dois lados do filme. Um feixe de luz com um comprimento de onda de incide perpendicularmente ao filme e a intensidade da reflexão é medida. A Fig. 35-46 mostra a intensidade em função do tempo ; a escala do eixo horizontal é . A intensidade muda por causa da evaporação nas duas superfícies do filme. Suponha que o filme é plano, que as duas superfícies do filme são paralelas e que o filme tem um raio de e um índice de refração de . Suponha também que o volume do filme diminui a uma taxa constante. Determine essa taxa.
Passo 1
O enunciado fala sobre um filme fino de espessura variável (devido à evaporação). Foi dado o gráfico de intensidade em função do tempo e queremos a taxa da variação do volume do filme.
O volume do filme é o volume de um cilindro de raio e espessura :
Assim,
Desta forma, para achar a taxa de variação do volume, precisamos da taxa de variação da espessura do filme!
Passo 2
Note que na reflexão do ar para o filme, há inversão de fase, porém na reflexão do filme para o ar não. Assim, devemos adicionar na defasagem:
A diferença de caminho será o dobro da espessura: . Além disso, como :
Vamos estudar os pontos em que a interferência é destrutiva (intensidade nula):
Assim,
Portanto,
Passo 3
Do gráfico vemos que o tempo entre dois mínimos consecutivos ( e ) é
A variação de espessura correspondente é
Portanto,
Assim,
Logo,