Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 30

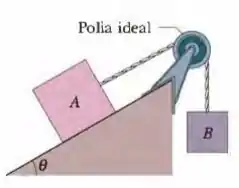
Na Fig. 6-33, dois blocos estão ligados por um fio que passa por uma polia. A massa do bloco A é 10   k g e o coeficiente de atrito cinético entre A e a rampa é 0,20 . O ângulo θ da rampa é 30 ° . O bloco A desliza para baixo ao longo da rampa com velocidade constante. Qual é a massa do bloco B ?

Passo 1

Belezera galera, se a gente desenhar as forças que atuam no sistema, vamos obter um desenho mais ou menos assim:

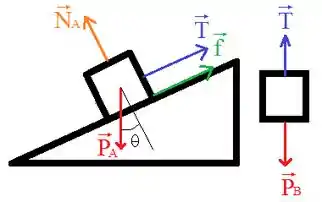
Com auxílio da ilustração, podemos aplicar a segunda lei de Newton para cada bloco. Vamos começar analisando o bloco A , lembrando que, como os blocos se movimentam com velocidade constante, a aceleração é nula. Assim, para cada eixo temos:

e i x o   x :       T + f - P A sin ⁡ θ = 0       e q . 1

e i x o   y :       N A - P A cos ⁡ θ = 0       e q . 2

Lembrando que a força de atrito cinética pode ser definida por:

f k = μ k N       e q . 3

Aplicando agora a segunda lei de Newton para o bloco B :

e i x o   y :       T - P B = 0     e q . 4

Passo 2

Inicialmente vamos determinar o valor da força de atrito. Para tanto, vamos isolar a normal na e q . 2 :

N A = P A cos ⁡ θ

Assim:

f k = μ k P A cos ⁡ θ       e q . 5

Passo 3

Substituindo na e q . 1 a e q . 5 e isolando T :

T = P A sin ⁡ θ - μ k P A cos ⁡ θ       e q . 6

Substituindo a e q . 6 na e q . 4 :

P A sin ⁡ θ - μ k P A cos ⁡ θ - P B = 0

m A g sin ⁡ θ - μ k m A g cos ⁡ θ - m B g = 0

Isolando m B , dividindo tudo por g e substituindo os valores conhecidos:

m B = 10 × sin ⁡ 30 ° - 0,20 × 10 × cos ⁡ 30 °

m B = 3,3   k g

Resposta

m B = 3,3   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jogador de beisebol de massa m=79k g , deslizando para chegar à segunda base, é retardado por uma força de atrito de módulo 470N . Qual é o coeficiente de atrito cinético μ k entre o jogador e o ch
Um porco brincalhão escorrega em uma rampa com uma inclinação de 35 ° e leva o dobro do tempo que levaria se não houvesse atrito. Qual é o coeficiente de atrito cinético entre o porco e a rampa?
As misteriosas pedras que migram. Na remota Racetrack Playa, no Vale da Morte, Califórnia, as pedras às vezes deixam rastros no chão do deserto, como se estivessem migrando (Fig. 6 -18). Há muitos ano
Um bloco de 3,5k g é empurrado ao longo de um piso horizontal por uma força F → de módulo 15N que faz um ângulo θ =40 ° com a horizontal (Figura 6-19). O coeficiente de atrito cinético entre o bloco e
Uma pessoa empurra horizontalmente um caixote de 55k g com uma força de 220N para deslocá-lo em um piso plano. O coeficiente de atrito cinético é 0,35 . (a) Qual é o módulo da força de atrito? (b) Qua