Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 6

Um porco brincalhão escorrega em uma rampa com uma inclinação de 35 ° e leva o dobro do tempo que levaria se não houvesse atrito. Qual é o coeficiente de atrito cinético entre o porco e a rampa?

Passo 1

Fala galerinha bonita, tudo joinha?!!

Se liga só nesse questão aqui, o enunciado diz que um porco brincalhão desce uma rampa inclinada com θ = 35 ° . A malandragem da questão é que ele diz que o porco demora o dobro do tempo pra escorregar na rampa caso ela não tivesse atrito, e sabendo apenas disso, ele nos pede pra encontrar o coeficiente de atrito da rampa:

Mas calma aí meu aprovado, pra começar podemos dazer o diagrama a seguir de forças que agem sobre o porco. Tal que:

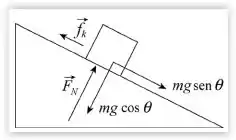
Aplicando a Segunda Lei de Newton aos eixos x e y , temos que:

m g sen ⁡ θ - f → k = m a

F → N - m g cos ⁡ θ = 0

Resolvendo esse sistema de equações e sabendo que f k = μ k F N , temos:

a = g ( sen ⁡ θ - μ k sen ⁡ θ )

Passo 2

Para calcular o tempo que o porco leva para percorrer uma distância l podemos usar a relação:

l = v 0 t + a t 2 2

t =   2 l a

Chamando de t ' o tempo que o porco leva para percorrer a mesma distância l em uma rampa sem atrito e de a ' a aceleração correspondente, temos que :

t t ' = 2 l a 2 l a '   = a ' a

o que nos leva a concluir que se t / t '   =   2 , a ' =   4 a . Como, de acordo com a Segunda Lei de Newton, a '   =   g   s e n   θ , temos:

g sen ⁡ θ = 4 g ( sen ⁡ θ - μ k cos ⁡ θ )

Resolvendo a equação acima para θ = 35 ° , obtemos μ k = 0,53

Resposta

μ k = 0,53

Tranquilo galera??? Bora resolver mais questões então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de 4,10k g é empurrado sobre um piso por uma força horizontal constante de módulo 40,0N . A Fig. 6-30 mostra a velocidade v do bloco em função do tempo t quando o bloco se desloca sobre o pis
Quando os três blocos da Fig. 6-29 são liberados a partir do repouso, aceleram com um módulo de 0,500m / s 2 . O bloco 1 tem massa M , o bloco 2 tem massa 2 M e o bloco 3 tem massa 2 M . Qual é o coef
Na Fig. 6-33, dois blocos estão ligados por um fio que passa por uma polia. A massa do bloco A é 10k g e o coeficiente de atrito cinético entre A e a rampa é 0,20 . O ângulo θ da rampa é 30 ° . O bloc
Você depõe como perito em um caso envolvendo um acidente no qual o carro A bateu na traseira de um carro B que estava parado em um sinal vermelho no meio de uma ladeira (Fig. 6-25). Você descobre que
Um fio de arame de comprimento 2 l é dobrado ao meio, formando um ângulo de 60 ° , e é suspenso pelo vértice O , oscilando num plano vertical. Calcule o período τ de pequenas oscilações em torno da po