Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 68
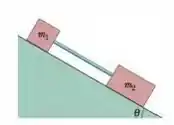
Na Fig. 6-46, uma caixa com formigas vermelhas (massa total ) e uma caixa com formigas pretas (massa total ) deslizam para baixo em um plano inclinado, ligadas por uma haste sem massa paralela ao plano. O ângulo de inclinação é . O coeficiente de atrito cinético entre a caixa com formigas vermelhas e a rampa é ; entre a caixa com formigas pretas e a rampa é . Calcule (a) a tensão da haste e (b) o módulo da aceleração comum das duas caixas. (c) Como as respostas dos itens (a) e (b) mudariam se as posições das caixas fossem invertidas?
Passo 1
A primeira coisa que devemos fazer é construir os diagramas de corpo livre das duas caixas:
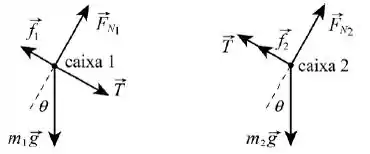
Para cada bloco, escolhemos um eixo encosta abaixo e um eixo na direção da força normal. Aplicando a Segunda Lei de Newton aos eixos e das duas caixas, obtemos quatro equações:
que, combinadas com a equação , descrevem totalmente a dinâmica do sistema.
Resolvendo o sistema de equações acima, obtemos:
Passo 2
Dessa forma obtemos a aceleração do sistema dada por :
Passo 3
Inverter a posição das caixas equivale a trocar os índices. A equação obtida no item (a) mostra que essa troca leva a um valor negativo para , com o mesmo módulo de antes , uma vez que :
E temos que .
Assim, a situação permanece a mesma, exceto pelo fato de que a haste passa a estar sob compressão e não sob tração como na situação anterior.
Tranquilo galera? Bora resolver mais questões então!
Resposta
Ei, a resposta está no passo a passo :)