Um bloco de aço de repousa em uma mesa horizontal. O coeficiente de atrito estático entre o bloco e a mesa é . Uma força é aplicada ao bloco. Calcule, com três algarismos significativos, o módulo da força se ela coloca o bloco na iminência de deslizar quando é dirigida (a) horizontalmente, (b) para cima, formando um ângulo de com a horizontal e (c) para baixo, formando um ângulo de com a horizontal.
Passo 1
a) Olá, querido! Cê está bem? Então, ele quer saber o módulo da força em várias situações.
A primeira é onde empurra um bloco horizontalmente e ele está na eminência de deslizar.
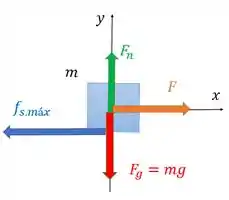
Bom pessoal, quando o bloco está na iminência de deslizar, a força de atrito é de atrito estático máximo dada por . E pela segunda lei de Newton na direção , onde porque não há movimento, a gente tem:
Passo 2
Mas quem é ?
Fazendo a segunda lei de Newton para o eixo , onde também temos :
Como :
Substituindo isso na equação do passo anterior:
Substituindo os dados
Passo 3
b) Agora aponta para cima formando com a horizontal.

Novamente há eminência de movimento, então a força de atrito é máxima. E pela segunda lei de Newton na direção , onde porque não há movimento, a gente tem:
Percebe que agora temos apenas uma componente de porque ela está inclinada. Vamos usar nela porque está colado no eixo . Escrevendo as expressões de cada uma das forças:
Passo 4
Novamente falta . Bora aplicar a segunda lei de Newton no eixo :
Percebe que agora temos uma componente de aqui também. Ela vai valer e fica positiva porque aponta para cima. E como :
Substituindo isso na equação do passo anterior:
Isolando e substituindo os dados
Passo 5
c) Agora aponta para baixo formando com a horizontal.
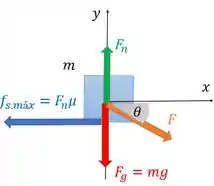
Novamente há eminência de movimento, então a força de atrito é máxima. E pela segunda lei de Newton na direção , onde porque não há movimento, a gente tem:
Percebe que agora temos apenas uma componente de aqui também porque ela está inclinada. Vamos usar nela porque está colado no eixo . Escrevendo as expressões de cada uma das forças:
Passo 6
Novamente falta . Bora aplicar a segunda lei de Newton no eixo :
Percebe que agora temos uma componente de aqui também. Ela vai valer e fica negativa porque aponta para baixo. E como :
Substituindo isso na equação do passo anterior:
Isolando e substituindo os dados
Tranquilo galera??? Bora resolver mais questões então!!!!!!
Resposta
a)
b)
c)