Projetando uma curva de uma rodovia. Se um carro entra muito depressa em uma curva, tende a derrapar. No caso de uma curva compensada com atrito, a força de atrito que age sobre um carro em alta velocidade se opõe à tendência do carro de derrapar para fora da estrada; a força aponta para o lado mais baixo da pista ( o lado para o qual a água escoaria). Considere uma curva circular de raio e um ângulo de compensação , na qual o coeficiente de atrito estático entre os pneus e o pavimento é . Um carro (sem sustentação negativa) começa a fazer a curva, como mostra a Fig.6-11. (a) Escreva uma expressão para a velocidade do carro , que o coloca na iminência de derrapar. (b) Plote, no mesmo gráfico, vomí, em função de para o intervalo de a , primeiro para (pista seca) e depois para (pista molhada). Calcule , em , para um ângulo de compensação e para (c) e (d) . (Agora você pode entender porque ocorrem acidentes nas curvas das estradas quando os motoristas não percebem que a estrada está molhada e continuam dirigindo na velocidade normal.)
Passo 1
Então galera , a gente sabe que um carro está na iminência de derrapar quando a força de atrito estático atinge o valor máximo, beleza?
Vamos considerar a soma vetorial da força de atrito com a força normal. Como as duas forças são perpendiculares e seus módulos são proporcionais , faz um ângulo , em que e é o ângulo de compensação da curva. Como a força centrípeta está na mesma direção da soma vetorial de com a força da gravidade , temos a seguinte relação:
Isolando na equação acima , obtemos :
Passo 2
Bom pessoal , o gráfico pedido com em radianos é descrito por :
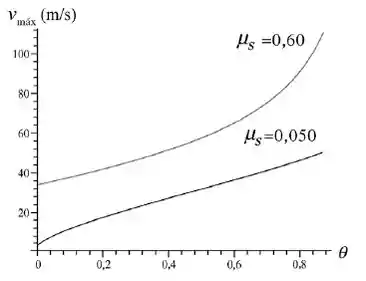
Beleza pessoal? Bora continuar que ainda não acabou!
Passo 3
Utilizando a equação achada no item (a) :
Para e , obtemos que :
Passo 4
Da mesma forma que no item anterior , utilizando a equação achada no item (a) :
Para e , obtemos que :
Tranquilo galera??? Boraresolver mais questões então
Resposta
Ei, a resposta está no passo a passo :)