Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 60
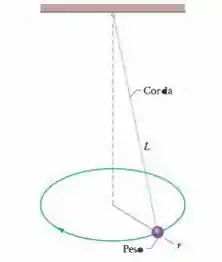
A Fig. 6-53 mostra um pêndulo cônico, no qual um peso (pequeno objeto na extremidade inferior da corda) se move em uma circunferência horizontal com velocidade constante. (A corda descreve um cone quando o peso gira.) O peso tem uma massa de , a corda tem um comprimento e a massa desprezível e o peso descreve uma circunferência de . Determine (a) a tensão da corda e (b) o período do movimento.
Passo 1
Bom pessoal , se o peso descreve uma circunferência de , a distância horizontal entre o peso e o eixo de rotação é dada por . Usando a trigonometria básica , sabemos que o ângulo que a corda faz com a horizontal é dado por :
A componente vertical da tensão da corda é e deve ser igual à força da gravidade . Assim,
Até aqui de boa? Bora continuar então!
Passo 2
Como a componente horizontal da tensão da corda é a força centrípeta, cujo módulo é , temos que , o que nos dá . O período por sua vez , pode ser obtido diividindo o comprimento da circunferência pela velocidade , sendo assim :
Resposta
Tranquilo pessoal??? Bora resolver mais questões então