Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.Problemas Adicionais - Ex. 94

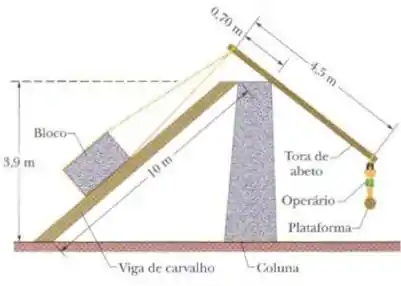
Até hoje se discute de que forma os pesados lintéis (blocos horizontais de pedra) foram colocados sobre blocos verticais em Stonehenge. Um possível método foi testado em uma pequena cidade tcheca. Um bloco de concreto com uma massa de foi puxado para cima ao longo de duas vigas de carvalho cujas superfícies superiores tinham sido descascadas e lubrificadas com gordura (veja a figura). As vigas tinham de comprimento e iam do chão até o alto de um dos blocos verticais que serviriam de apoio para o bloco a ser levantado. Os blocos verticais tinham de altura; o coeficiente de atrito estático entre o bloco e as vigas era . O bloco foi puxado por cordas enroladas no bloco, que passavam pela extremidade superior de duas toras de abeto de de comprimento. Uma plataforma foi instalada na extremidade oposta de cada tora. Quando um número suficiente de operários subia na plataforma, a tora correspondente girava em torno de um apoio no alto da pedra vertical em que se apoiava e puxava uma extremidade do bloco por uma pequena distância ao longo da viga. Para cada tora, a corda que envolvia o bloco era aproximadamente perpendicular à tora; a distância entre o ponto de apoio e o ponto em que a corda estava amarrada na tora era de . Supondo que cada operário tinha uma massa de , determine o menor número de operários que deviam se posicionar sobre as duas plataformas para que o bloco começasse a se mover para cima ao longo das traves. (Na realidade, metade deste número de operários poderia deslocar o bloco, movendo primeiro uma das extremidades e depois a outra).

Passo 1

As forças que puxam o bloco para baixo são o atrito com a viga de carvalho e uma componente do peso:

Como estamos em um plano inclinado, a força normal é igual à outra componente () do peso:

Então:

Beleza, essa força vai realizar um torque sobre a tora de abeto. Considerando que ela age em um ponto a do apoio da tora na coluna, esse torque é:

Passo 2

Para que a tora de abeto começe a girar em torno do ponto, esse torque da força tem que ser, pelo menos, igual ao torque dos pesos dos operários.

Então vamos calcular . A força associada a ele depende do número de operários que estão pendurados:

E o ângulo que essa força forma com a tora de abeto é o complementar do ângulo que usamos lá em cima, então:

E a distância até o ponto de apoio é .

Passo 3

Agora é só igualar as duas expressões:

Mas , então:

Vamos dividir tudo por e substituir os valores das massas, , e :

E agora falta calcular o ângulo (a inclinação da viga de carvalho) mas para isso só precisamos olhar para a figura:

Então:

Isso quer dizer que precisamos de pelo menos operários.

Resposta

São necessários pelo menos operários.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bobina oca, cilíndrica e uniforme tem raio interno R / 2 , raio externo R e massa M (Fig. P10.70). Ela é montada de modo a girar em um eixo horizontal fixo. Um contrapeso de massam é conectado à p

Quando uma pessoa fica na ponta de um pé (uma posição difícil), a posição do pé é como mostrada na Figura P10.69a. A força gravitacional total F → g no corpo é suportada pela força normal n → exercida

Os ponteiros de horas e de minutos do Big Ben, o relógio da torre do Parlamento em Londres, têm 2,70m e 4,50m de comprimento e massas de 60,0k g e 100k g , respectivamente (consulte a Fig. P10.17). De

O grande músculo quadríceps na parte superior da perna termina em sua extremidade inferior em um tendão ligado à extremidade superior da tíbia (Fig. P10.77a). As forças sobre a parte inferior da perna

Uma esfera sólida de massa m e raio r rola sem escorregar ao longo da pista mostrada na Figura P10.83. Ela começa do repouso com o ponto mais baixo da esfera na altura h acima da base do aro de raio R