Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.6 - Ex. 25
Na Fig. 7-33, um pedaço de queijo de repousa no chão de um elevador de que é puxado para cima por um cabo, primeiro por uma distância m e depois por uma distância . (a) No deslocamento , se a força normal exercida sobre o bloco pelo piso do elevador tem um módulo constante qual é o trabalho realizado pela força do cabo sobre o elevador? (b) No deslocamento , se o trabalho realizado sobre o elevador pela força (constante) do cabo é , qual é o módulo de ?
Passo 1
Então galera, vamos começar desenhando um diagrama de forças para o sistema Elevador-Queijo e colocar nele as forças externas que atuam nesse sistema:
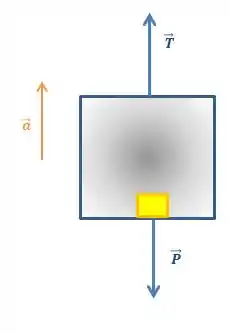
Aplicando a segunda lei de newton, teremos:
Aqui, precisamos estar atentos que esse sistema é elevador mais queijo, logo a massa vai ser
Bom, isso é tudo que dá pra ter por agora...
Passo 2
Na letra , temos que ao longo do deslocamento desse elevador, a força normal exercida sobre o queijo foi de ... se a gente fizer o diagrama de forças em cima do queijo, vamos encontrar a aceleração dele... e se liga, a aceleração dele, é a própria aceleração do elevador, afinal, eles fazem parte do mesmo sistema...
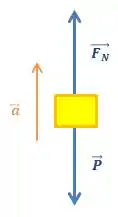
Aplicando a segunda lei de newton, teremos:
Show de bola, descobrimos portanto a aceleração do queijo e assim a aceleração do sistema elevador+queijo! Ela vale e aponta para cima... agora voltando para a nossa equação anterior...
e o trabalho realizado pelo cabo , por sua vez , é dado por :
Como a tração e o deslocamento apontam para cima, vamos ter apenas que:
De boa até aqui galera? Bora continuar que ainda não acabou!
Passo 3
Bom pessoal, na letra , temos que para o deslocamento , o trabalho será de ...
Agora, vamos fazer o mesmo processo, só que ao contrário...
Esse trabalho é dado por:
E como o deslocamento é para cima e a tração do cabo também está para cima, teremos então:
Portanto, a tração no cabo do elevador será de:
Show de bolê... com essa tração, podemos encontrar a aceleração do sistema elevador-queijo!
Só usar a segunda lei de newton...
Substituindo a nova tração:
Caramba, deu uma aceleração negativa!!
Não precisa criar pânico, isso só indica que nesse deslocamento, o elevador está freando... mas ele continua subindo normalmente, mas ao invés de estar acelerando, ele está desacelerando...
Agora, para encontrar a força normal, vamos voltar a segunda lei de newton, só que para o queijo:
Isso aí é aproximadamente...