Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.Problemas Adicionais - Ex. 69
Para empurrar um engradado de para cima em um plano inclinado de em relação à horizontal, um operário exerce uma força de paralela ao plano inclinado. Quando o engradado percorre , qual o trabalho realizado sobre ele (a) pela força aplicada pelo trabalhador, (b) pela força gravitacional e (c) pela força normal? (d) Qual é o trabalho total realizado sobre o engradado?
Passo 1
Oi, galerinha! Tudo bom? A grande sacada dessa questão é perceber que todas as forças que atuam no engradado são constantes, portanto, podemos usar a seguinte relação para calcular o trabalho de cada força:
Lembrando que a o trabalho total realizado sobre o engradado pode ser calculado somando o trabalho realizado por cada força individualmente. Como as forças que atuam no engradado são a força peso (), a força normal ()e a força que o operário () exerce sobre o engradado, então:
Mas antes de começarmos a calcular, bora fazer um esboço do desenho para ver melhor as forças atuantes:
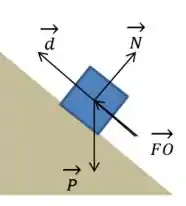
Bora lá!
Passo 2
- Calculando o trabalho da força que o operário exerce sobre o engradado, percebendo que esta força está agindo na mesma direção e sentido do deslocamento, então, , assim:
- Para calcular o trabalho do peso, devemos lembrar que o ângulo dado do plano inclinado é também o âgulo que a força peso faz com o eixo perpendicular ao movimento, portanto, para determinar o ângulo entre o peso e o deslocamento, devemos somar ao ângulo do plano inclinado dado, tendo em vista que o deslocamento está sendo para cima. Assim:
- A força normal está perpendicular ao deslocamento, portanto, e o cosseno de é nulo. Assim:
- O trabalho total é, portanto:
Passo 3
Passo 4
Passo 5
Resposta
- ;
- ;
- .