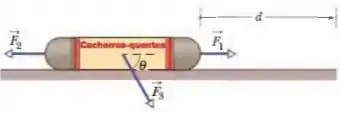
A Fig. 7-41 mostra um pacote de cachorros-quentes escorregando para a direita em um piso sem atrito por uma distância enquanto três forças agem sobre o pacote. Duas são horizontais e têm módulos e ; a terceira faz um ângulo para baixo e tem um módulo . (a) Qual é o trabalho total realizado sobre o pacote pelas três forças mais a força gravitacional e a força normal? (b) Se o pacote tem uma massa de e uma energia cinética inicial igual a zero, qual é sua velocidade no final do deslocamento?
Passo 1
Primeiro, devemos percerber que todas as forças que atuam sobre um pacote de cachorro quente são constantes. Então, para calcular o trabalho de qualquer uma destas forças, podemos usar:
Aqui, devemos perceber que as forças que atuam na direção perpendicular ao plano não realizam trabalho, pois o cosseno entre a força e o deslocamente será nulo. Portanto, a normal e o peso não realizam trabalho neste deslocamento.
Além disso, devemos percer que o deslocamento está dado em centímetros e, por isso, devemos multiplicar o deslocamento por um fator de para fazer a conversão de para .
Por fim, devemos lembrar do teorema trabalho-energia cinética, que será fundamental para determinarmos a velocidade no final do deslocamento:
Passo 2
Primeiro, vamos calcular o trabalho para cada força não perpendicular ao deslocamento usando a . Iniciando pelo trabalho realizado pela força :
Para :
Para :
Portanto, o trabalho total será:
Passo 3
Para determinar a velocidade final do pacote, vamos usar a :
Sabendo que foi calculado no passo anterior e a energia cinética inicial é nula, então:
Isolando :
Resposta
- ;
- .