Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.4 - Ex. 4
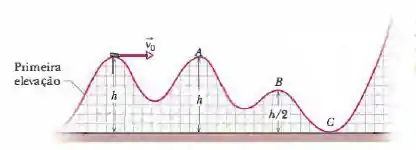
Na Fig. 8-27, um carro de montanha-russa de massa atinge o cume da primeira elevação com uma velocidade a uma altura . O atrito é desprezível. Qual é o trabalho realizado sobre o carro pela força gravitacional entre este ponto e (a) o ponto , (b) o ponto e (c) o ponto ? Se a energia potencial gravitacional do sistema carro-Terra é tomada como nula em , qual é o seu valor quando o carro está (d) em e (e) em ? Se a massa é duplicada, a variação da energia potencial gravitacional do sistema entre os pontos e aumenta, diminui ou permanece a mesma?
Passo 1
Oi, galerinha! Tudo bom? Essa é uma questão de conservação de energia. Para resolve-la temos que lembrar que o trabalho realizado pelo peso pode ser relacionado pela variação da sua energia potencial através de:
Reescrevendo a variação da energia potencial, temos:
Aqui percebemos que só há trabalho se houver variação de altura.
Passo 2
Como o ponto inicial e o ponto possuem a mesma altura, então pela podemos afirmar que o trabalho entre esses dois pontos é zero, pois:
Substituindo na
Passo 3
b) Vamos usar novamente a , agora para determinar o trabalho entre o ponto inicial e o ponto :
Repara que a altura do ponto é metade da inicial,
Passo 4
c) Faremos de maneira análoga a anterior para calculcar o trabalho entre o ponto inicial e ponto :
Repara que a altura no ponto é zero,
Passo 5
d) Quando ele fala que em a energia potencial é nula, usamos ali como nossa origem para . Assim, para calculcar a energia potencial para os pontos :
E para o ponto :
Passo 6
e) Como a variação da energia potencial é:
Se a massa for dobrada, então a variação da energia potencial também será dobrada.
Resposta
- ;
- ;
- ;
- ;
- ;
- .