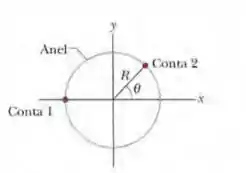
A Fig. 22-39 mostra um anel de plástico de raio . Duas pequenas contas coloridas estão sobre o anel: a conta 1, de carga , que é mantida fixa na extremidade esquerda, e a conta 2, de carga , que pode ser deslocada ao longo do anel. As duas contas produzem, juntas, um campo elétrico de módulo no centro do anel. Determine (a) um valor positivo e (b) um valor negativo do ângulo para que
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema foi dado um sistema de partículas carregadas e nosso objetivo é obter um angulo positivo e outro negativo para que o campo elétrico no centro do sistema seja.
Para isso, vamos calcular as componentes e do vetor campo elétrico devido as contas 1 e 2 usando decomposição do vetor campo elétrico, que assumirá uma configuração nesse estilo aqui.
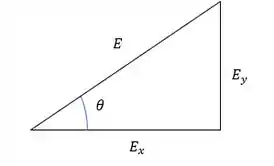
Aqui usaremos as seguintes decomposições.
E no fim vamos relacionar essa resultante conhecida com o ângulo usando o teorema de Pitágoras e um pouco de trigonometria.
Sacou? Bora começar! 😉
Passo 2
Primeiramente, iremos calcular a componente x. Para isso, devemos lembrar que como a conta 2 não está no eixo x, para calcular a componente x devemos decompor o vetor campo elétrico no eixo x, isto é, multiplicar por . Calculando a componente x do campo elétrico:
Agora, para a componente y, basta a gente multiplicar o vetor campo elétrico da conta 2 por isto é, decompor no eixo y. Como a conta 1 está no eixo x, ela não tem componente y. Então:
Tranquilo até aqui? 😬
Passo 3
Agora devemos calcular o campo elétrico total, que é somar os quadrados das componentes e tirar a raiz disso, que nada mais é do que fazer o Pitágoras do triangulo do ínicio.
Elevando ao quadrado, e simplificando, temos:
Deixando explicitado:
Substituindo pelos valores numéricos que já temos, lembrando da constante de Coulomb (, obtemos dois valores de ângulo possível, um positivo e um negativo:
Dessa forma os dois ângulos que possuem o cosseno são
a) O valor positivo é .
b) O valor negativo é
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta
a) O valor positivo é .
b) O valor negativo é