Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 24.Exercícios e Problemas - Ex. 8
Na Fig 24-24, as cargas estão localizadas nos vértices de um triangulo equilátero. Para que valor de Q (sinal e módulo) o campo elétrico resultante se anula no ponto C, o centro do triângulo?
Passo 1
Vamos lá turminha da fenda do biquini, o primeiro passo é realizar uma análise geométrica do triangulo de forma a encontrar as distancias dos vértices em relação ao centro.
Assumindo A, B e C como vértices e O como centro do nosso triângulo de estudo.
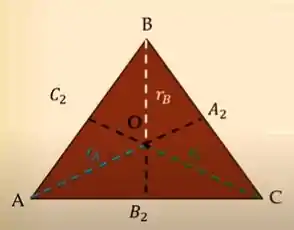
Passo 2
Agora migos e migas vamos encontrar os valores de que são as distancias dos vértices em relação ao centro. Para um triângulo equilátero a tamanho de cada uma de suas medianas é:
No nosso caso o , então:
E como:
Por ser equilátero temos que , aí agora teremos:
Passo 3
Cola em mim aqui e que você vai entender, vem comigo, por que agora vamos encontrar a intensidade dos campos elétricos dos vértices A e C, que possuem o a mesma carga , então , dessa forma:
Passo 4
Agora temos que analisar o campo vetorialmente, primeiro olha o pula do gato (miau!) no eixo X o campo produzido por uma carga no vértice B é anulado, ficando apenas a componente no eixo Y, por isso vamos analisar apenas esse eixo:
Daí vamos encontrar a componente Y dos campos :
Passo 5
Como o objetivo é que o campo seja nulo, temos , e agora podemos encontrar:
Resposta
Substituindo os valores numéricos para a equação do Passo 5, temos: