Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 2º - Capítulo 3.Problemas - Ex. 2

Um modelo clássico de uma molécula ionizada é constituído por um par de partículas fixas, ambas de carga + e , separadas por uma distância 2 a com uma terceira partícula de carga - e , massa m , descrevendo uma órbita circular de raio ρ em torno do eixo que liga as as duas outras cargas. Obtenha: (i) O campo elétrico que atua sobre a carga - e ; (ii) a relação entre o raio e a frequência angular de revolução ω .

Passo 1

Fala galera, tudo tranquilo? Vamos para mais um problema de eletricidade. Para começar, vamos montar nosso diagrama, que por sinal é bem parecido com o problema 4 ou problema 9 do capítulo anterior. Nosso primeiro diagrama é dado na figura abaixo

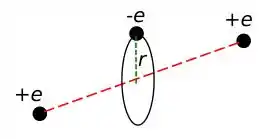
Este é o nosso tipo de problema. Agora iremos decompor os vetores campo elétrico cada carga exerce na carga - e .

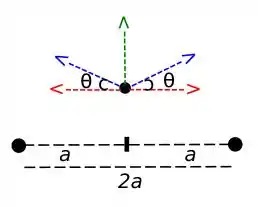
As linhas em azul são os campos elétricos das cargas que estão atuando na carga que se encontra acima. Vamos chamar as cargas de q1 (carga da esquerda), q2 (carga da direita) e q3 (carga que está no meio). Observe que na componente x, as linhas em vermelho estão opostas, o que nos garante que os campos E → x 1 e E → x 2 se anulam. Já na componente y, o campo é dado pela linha verde, a qual comporta a soma dos dois campos em y.

E → y = E → y 1 + E → y 2

As componentes em y são as componentes que queremos trabalhar.

Pegando os vetores em Y, sabemos que as componentes que queremos são componentes em ĵ, com respeito ao seno do ângulo θ . O módulo dos campos E → y 1 e E → y 2 são iguais, o que nos leva a escrever a seguinte equação:

E → T o t a l   =   E → y 1 s e n ( θ )   +   E → y 2 s e n ( θ ) = 2 E → y s e n ( θ ) , este seno de teta é dado por

s e n ( θ )   =   ρ d ,   o n d e   d =   ( a ²   +   ρ ² ) 1 / 2 . Essa expressão você pode encontrar ao formar um triângulo a partir das distâncias que ligam as cargas. Se você acompanhar a linha tracejada em azul, ela é considerada nossa distância “d”, enquanto que “a” seria a distância horizontal até a partícula q3.

Nossa equação para o campo agora é da forma:

E → T o t a l = 2   K   Q d 2   ρ d = 2   K   Q   ρ d 3 = 2   K   Q   ρ ( ρ 2 +   a 2 ) 3 / 2

Passo 2

Para o item (ii), ele pede uma relação entre o raio ρ e a frequência de revolução ω . Você pode lembrar do problema 3 do capítulo 2 onde ele relaciona as forças elétrica e centrípeta. Iremos fazer o mesmo neste caso.

F → = E → T o t a l   q = m e ω ²   ρ

Assim nossa frequência de revolução é dada na seguinte equação:

ω = E → T o t a l   q m e   ρ 1 / 2

Resposta

(i) E → T o t a l = 2   K   Q d 2   ρ d = 2   K   Q   ρ d 3 = 2   K   Q   ρ ( ρ 2 +   a 2 ) 3 / 2

(ii) ω = E → T o t a l   q m e   ρ 1 / 2

Exercícios de Livros Relacionados

Na Fig. 22-31, as quatro partículas são mantidas fixas e têm cargas q 1 = q 2 = + 5 e , q 3 = + 5 e e q 4 = - 12 e . A distância d = 5,0μ m . Qual é o módulo do campo elétrico no ponto P ?
Um condutor em forma de anel com raio a=2,5 cm possui uma carga positiva Q=+0,125 nC uniformemente distribuída ao longo do anel, como indica a figura 21.24. O centro do anel está na origem O do sistem
A molécula de amônia ( N H 3 ) possui um momento de dipolo elétrico igual a 5 ∙ 10 - 30C ∙ m . Moléculas de amônia na fase gasosa são colocadas em um campo elétrico uniforme E → cujo módulo é igual a
Uma carga q 1 = + 5n C é colocada na origem de um sistema de coordenadas e uma carga q 2 = 2n C é colocada no lado positivo do eixo x , no ponto x = 4c m .(a) Se uma terceira carga q 3 = 6n C é coloca
Um fio plástico retilíneo e não condutor de 8,5c m de comprimento carrega uma densidade de carga de + 175n C / m , distribuída uniformemente ao longo do comprimento. Eles está sobre a superfície horiz