Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 20.Exercícios e Problemas - Ex. 8

A Figura 20.13 mostra um cone feito de material com resistividade ρ , com a ponta aparada por um plano paralelo à base. As duas faces circulares do corpo têm raios a e b , e forma metalizadas. Supondo que ρ seja muito maior do que a resistividade do metal depositado nas faces circulares, calcule a resistência elétrica entre aquelas faces.

Passo 1

Antes de resolver o problema, considere o seguinte problema de geometria:

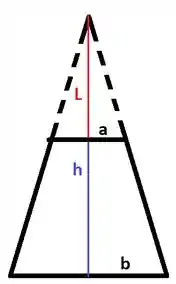
Queremos escrever L em função de a , b e h . Usando semelhança de triângulos:

L a = L + h b → L b = L a + h a

Logo,

L b - a = h a

Portanto,

L = h a b - a

Passo 2

Para calcular a resistência desse objeto vamos considerar que ele é composto por vários disquinhos bem fininhos de espessura d y . A seguir desenho um desses discos, com raio x a uma distância y da base:

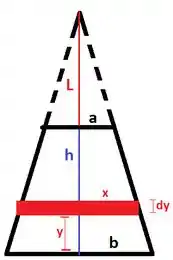
Vamos relacionar y e x por semelhança de triângulo:

L a = L + h - y x

Logo,

x = a L L + h - y

Substituindo a expressão de L que encontramos no passo 1:

x = a b - a h a h a b - a + h - y

Assim,

x = b - a h h a + h b - h a - b y + a y b - a

Portanto,

x = h b - b - a y h = b - b - a h y

Passo 3

A resistência infinitesimal desse disquinho será

d R = ρ A d i s c o d y

Note que essa é a versão R = ρ L / A para o disquinho. Como A d i s c o = π x 2 , temos que

A d i s c o = π b - b - a h y 2

Com isso,

d R = ρ π ⋅ 1 b - b - a h y 2 d y

Para achar a resistência, basta integrar y de 0 até h :

R = ∫ 0 h ρ π ⋅ 1 b - b - a h y 2 d y

Para fazer essa integral fazemos a seguinte mudança de variável:

x = b - b - a h y → d x = - b - a h d y

Assim,

d y = - h b - a d x

Quando y = 0 , temos x = b . Já para y = h , achamos x = a :

R = - ρ π ⋅ h b - a ∫ b a 1 x 2 d x = ρ h π b - a ∫ a b 1 x 2 d x

Fazendo a integral, achamos

R = ρ h π b - a ⋅ 1 a - 1 b

Desta forma,

R = ρ h π a b

Resposta

R = ρ h π a b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio com seção transversal de área A , comprimento L 1 , resistividade ρ 1 e coeficiente de temperatura α 1 , é conectado nas duas extremidades a um segundo fio que tem a mesma seção transversal, co
A resistividade do tungstênio aumenta de forma aproximadamente linear com a temperatura de 56,0n Ω ⋅ m a 293K para 1,10μ Ω ⋅ m a 3500K . Uma lâmpada recebe energia de uma fonte dc de 100 V. Sob estas
Um bastão de tungstênio tem 50 cm de comprimento e uma seção transversal quadrada com lados de 1,0 mm. (a) Qual é sua resistência a 20°C? (b) Qual é sua resistência a 40°C?
O espaço entre duas cascas esféricas metálicas concêntricas é preenchido com um material que tem resistividade de 3,50 × 10 - 5Ω ⋅ m . Se a casca metálica interna tem um raio externo de 1,50c m e a ca
Um resistor de Nichrome de 10,0Ω é ligado em um circuito eletrônico usando finos fios de cobre com diâmetro de 0,600m m . Os fios de cobre têm comprimento total de 50,0c m . (a) Que resistência adicio