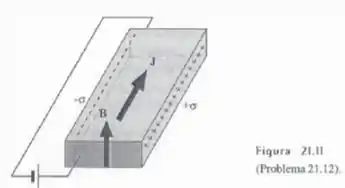
A Figura 21.11 mostra uma barra conduzindo corrente com uma densidade ortogonal a um campo magnético . Suponha que os portadores de corrente tenham cargas positivas e que sua densidade seja . (a) Mostre que em um regime permanente as duas faces indicadas na figura acumulam densidade de cargas que neutralizam a força de Lorentz. (b) Mostre que o campo elétrico ortogonal a é dado pela equação 21.31. (c) Calcule o valor de .

Antes de começarmos a discutir o problema, considere a dimensões marcadas na figura:

A corrente que flui no fio é dada pelo produto de com a área :

Podemos relacionar também a densidade de corrente com a velocidade de cada portador de carga por

A força magnética que atua sobre cada carga é dada pela força de Lorentz:

Com o sistema de coordenadas que eu adotei na figura, temos que

Assim,

Escrevendo em termos da corrente, temos que

Com isso, as cargas positivas vão se deslocar para a direita (direção ) e haverá um acúmulo de carga positiva na superfície lateral direita, indicada por na figura. Já na superfície lateral esquerda, haverá um acúmulo de carga negativa, com densidade superficial .

Isso vai fazer com que apareça um campo elétrico uniforme na direção :

Esse campo é igualzinho o campo de um capacitor de placas paralelas:

Com isso, vai aparecer uma força elétrica sobre as cargas , dada por

Essa força vai anular a força magnética, que é exatamente o que o exercício pediu para gente mostrar no item (a)!