Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Exercício - Ex. 19

Na figura 24.26, seja C 1 = 3,0   μ F e V a b = 120   V . A carga no capacitor C 1 é igual a 150 μ C . Calcule a voltagem através dos outros dois capacitores.

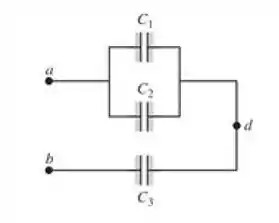
Passo 1

Temos para associação de capacitores:

i ) C a p a c i t o r e s   e m   p a r a l e l o :

C 12 = C 1 + C 2

Q 12 = Q 1 + Q 2

V 1 = V 2 = V 12

i i ) C a p a c i t o r e s   e m   s é r i e :

1 C e q = 1 C 12 + 1 C 3

Q 12 = Q 3 = Q

V = V 12 + V 3

Passo 2

Como C 1 e C 2 estão em paralelo V 1 = V 2 .

Além disso sabemos a carga e capacitância de C 1 .

V 1 = V 2

V 2 = Q 1 C 1

V 2 = 150 ⋅ 10 - 6   3 ⋅ 10 - 6  

V 2 = 50   V

Passo 3

Como C 3 está em série com C 1 e C 2 temos:

V a b = V 1 + V 3

V 3 = V a b - V 1

V 3 = 120 - 50

V 3 = 70   V

Resposta

V 2 = 50   V , V 3 = 70   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera de metal carregada, com 10 cm de diâmetro, tem uma energia potencial de 8000 V em relação a V = 0 no infinito. Calcule a densidade de energia do campo elétrico perto da superfície da esfera
Qual é a energia armazenada em 1,00m 3 de ar em um dia de “tempo bom”, no qual o módulo do campo elétrico da atmosfera é 150V / m ?
Qual é a capacitância necessária para armazenar uma energia de 10k W·h com uma diferença de potencial de 1000V ?
Uma grande superfície plana e não-condutora tem densidade de carga, σ , uniforme. Foi feito um pequeno furo circular de raio R , no centro da superfície, conforme mostrado na Fig. 27-35. Desprezando-s
A Fig. 27-36 mostra a seção transversal de um tubo metálico longo, de parede fina, de raio R com carga por unidade de comprimento λ em sua superfície. Determine expressōes de E para várias distâncias