Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 73
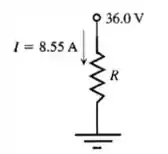
A Figura 26.75 mostra uma convenção geralmente usada nos diagramas de circuitos. A bateria (ou outra fonte de tensão) não é mostrada explicitamente. Fica implícito que o ponto no topo do diagrama, indicado com o dístico , está conectado ao terminal positivo de uma bateria de que possui resistência interna desprezível; e o ponto indicado na parte inferior simboliza a “terra” e está conectado ao terminal negativo da bateria. Embora não indicado explicitamente, o circuito é completado pela bateria. (a) Qual é a diferença de potencial do ponto em relação ao ponto quando a chave está aberta? (b) Qual é a corrente que passa pela chave quando ela está fechada? (c) Qual é a resistência equivalente do circuito quando a chave está fechada?
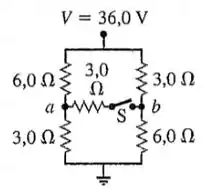
Passo 1
Vamo lá galera, essa questão é um tanto grande mas não vamos desistir! (a) O circuito é mostrado abaixo!
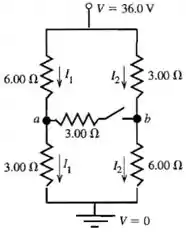
A queda potencial pelo ramo pararelo é de . Usaremos esse fato para calcular e . Logo, a potne do ponto para o ponto e vamos calcular com a corrente deles. Então simbora!
Para calcular começaremos no ponto até o ponto , somando todos os aumentos e as quedas de tensão até lá. Podemos fazer isso começando pelo resistor :
Passo 2
Agora temos vários caminhos de corrente, como mostrado na figura abaixo. Usaremos a regra da junção para escrever a corrente em cada caminho das três correntes , e . Aplicaremos a lei das malhas para as três malhas para achar as três equações para as três correntes!
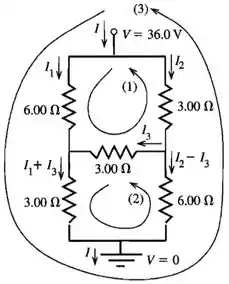
Indo pros cálculos, temos:
Loop 1:
Loop 2:
Relacionando isso, temos:
Loop 3:
e
Disso,
Logo, a corrente pelo interruptor é:
Passo 3
(c)Dos resultados no item (a) a corrente passando pela bateria é . O circuito equivalente é o um simples resistor produzindo a mesma corrente por uma bateria de 36V.
