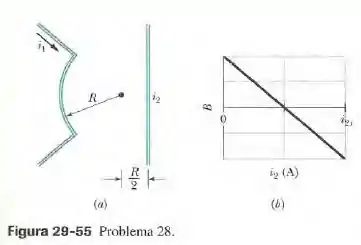
A figura 29-55a mostra dois fios. O fio 1 é formao por um arco de circunferência de raio R e dois segmentos radiais e conduz uma corrente no sentido indicado. O fio 2 é longo e retilíneo, conduz uma corrente que pode ser ajustada e está a uma distância do centro do arco. O campo magnético produzido pelas duas correntes é medido no centro da curvatura do arco. A figura 29-55b mostra a componente de na direção perpendicular ao plano do papel em função da corrente . A escala horizontal é definida por . Determine o ângulo subtendido pelo arco.

Para descobrirmos o campo magnético no ponto central podemos fazer o cálculo por trechos do objeto em questão. Vamos iniciar olhando as partes retilíneas. A lei de Biot-Savart nos diz o seguinte:

Para os dois elementos retilíneos, o ângulo entre é zero e . Portanto:

Assim, a contribuição de toda a parte reta para o campo magnético é zero.