Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.3 - Ex. 39

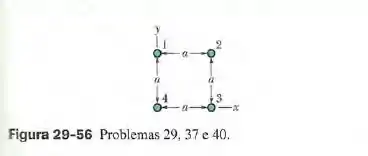
Na figura 29-56, quatro fios retilíneos longos são perpendiculares ao papel e suas seções retas formam um quadrado de lado a = 8,50   c m . Todos os fios conduzem correntes de 15,0   A para fora do papel. Em termos dos vetores unitários, qual é a força magnética por metro de fio que age sobre o fio 1?

Passo 1

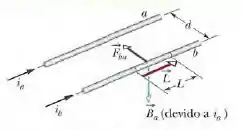
A força entre duas correntes paralelas na presença do campo magnético externo B → é dada por:

F b a → = i b L → × B a →

em que L → é o vetor comprimento do fio. Podemos ver na figura acima, os vetores L → e B a → são mutuamente perpendiculares e, portanto, de acordo com a equação para fios retilíneos longos, podemos escrever:

F b a = i b L B a s e n 90 ° = μ o L i a i b 2 π d F b a L = μ o i a i b 2 π d

Pela simetria do problema, apenasas forças (ou suas compoenetes) ao longo das diagonais contribuem para a força total. Fazendo θ = 45 ° e sando a expressão anterior:

F 1 = F 12 → + F 13 → + F 14 → = 2 F 12 c o s θ + F 13 F 1 = 2 μ o i 2 2 π a cos ⁡ 45 ° + μ o i 2 2 2 π a = 3 2 2 π μ o i 2 a F 1 = 3 2 2 π ⋅ 4 π × 10 - 7   T . m A 15,0   A 2 8,50 × 10 - 2   m F 1 = 1,12 × 10 - 3 N m

A força F 1 → aponta na direção r ^ = ( i ^ - j ^ ) / 2 . Na notação dos vetores unitário, temos:

F 1 → = 1,12 × 10 - 3 N m 2 i ^ - j ^ = 7,94 × 10 - 4 N m i ^ + - 7,94 × 10 - 4 N m j ^ F 1 → = 0,794   n N / m i ^ + ( - 0,794   n N / m ) j ^

Resposta

A força por unidade de comprimento é:

F 1 → = 0,794   n N / m i ^ + ( - 0,794   n N / m ) j ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula alfa ( um núcleo de He contendo dois prótons e dois nêutrons e possuindo massa igual a 6,64 × 10 - 27 k g ) se move horizontalmente a 35,6 km/s quando penetra o campo magnético vertical
Um núcleo de 16 O (carga + 8 e ) que se move horizontalmente do oeste para leste, com uma velocidade de 500 km/s, sofre uma força magnética de 0,00320 nN, orientada verticalmente de cima para baixo. D
Uma bateria de 150 V é conectada a duas placas metálicas paralelas, com área de 28,5 c m 2 , e distantes 8,20 m m entre si. Um feixe de partículas alfa (carga + 2 e , massa 6,64 × 10 - 27 k g ) é acel
Um feixe de prótons que se move a 1,20 km/s penetra um campo magnético uniforme, deslocando-se perpendicularmente ao campo. O feixe sai do campo magnético em um sentido perpendicular ao sentido origin
Reator nuclear. Quando dois núcleos de dêuteron (carga + e , massa 3,34 × 10 - 27 k g ) se aproximam o suficiente, a atração da força nuclear intensa vai fundi-las e produzir um isótopo de hélio, libe