Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 19
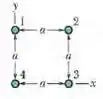
A figura 29-49 quatro fios retilíneos longos são perpendiculares ao papel e suas seções retas formam um quadrado de lado . As correntes são para fora do papel nos fios 1 e 4 para dentro do papel nos fios 2 e 3 e todos os fios conduzem uma corrente de . Em termos dos vetores unitários, qual é o campo magnético no centro do quadrado?
Passo 1
E aí, galerinha! 😉
Nesse problema temos quatro fios retilíneos longos perpendiculares ao papel e suas seções retas formam um quadrado de lado . As correntes são para fora do papel nos fios 1 e 4 para dentro do papel nos fios 2 e 3 e todos os fios conduzem uma corrente de . A partir daí queremos saber, em termos dos vetores unitários, qual é o campo magnético no centro do quadrado.
Lembra como fazemos isso? 🤔
Cada fio produz um campo no centro do quadrado de módulo:
(dado pela Lei de Ampére)
Sobre a direção do campo, este pode ser encontrado pela regra da mão direita.Por exemplo, para o fio que possui uma corrente saindo do plano da página, a regra da mão direita vai dar em algo mais ou menos assim:
Tranquilo até aqui? 😁
Passo 2
Realizando o mesmo procedimento para os demais fios, vamos chegar nas seguintes direções para os campos.
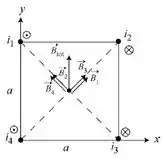
Repara que os campos produzidos por e estão na diagonal para direita e para cima e os campos produzidos por e estão na diagonal para esquerda e para cima.
Como os campos possuem o mesmo módulo, por simetria, as componentes horizontais irão se anulas, sobrando apenas as componentes verticais para formar o campo total (representado na figura acima como .
E a soma das componentes verticais é:
Ou seja
Substituindo os valores dados no enunciado...
E aí! entendeu tudo? Responde Aí! 😁
Resposta
O campo magnétido no centro do quadrado é: