Exercícios de Lei de Biot-Savart Geral - Lista de Exercícios Resolvida
Questão 1
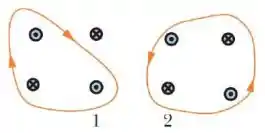
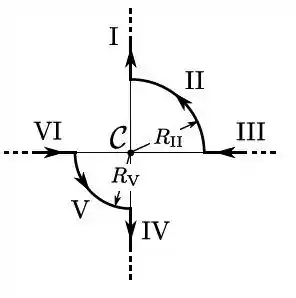
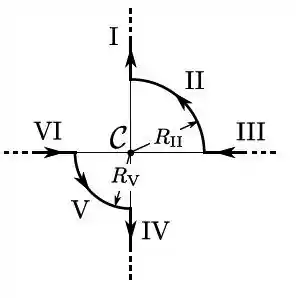
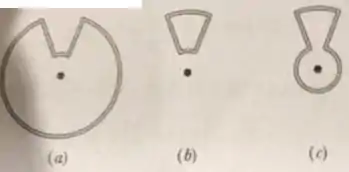
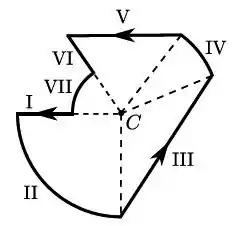
Considere o circuito da figura abaixo, constituído por segmentos retilíneos (I, III, V e VI) e segmentos de arco de círculos (II, IV e VII) concêntricos com o ponto , percorridos por uma corrente estacionária , com sentido assinalado. Indique quais de tais segmentos dão uma contribuição não nula para o campo magnético resultante no ponto .
- II, III, IV, V e VII
- I, III, V e VI
- II, IV e VII
- I, II, IV, VI e VII
- Todos criam campo magnético não nulo em
Questão 2
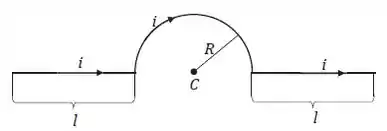
Mostre que o módulo do campo magnético produzido no centro de uma espira retangular de comprimento e largura , percorrida por uma corrente é dado por:
Ver solução completaQuestão 3
Determine o módulo do campo magnético de um fio retilíneo de comprimento , por onde passa uma corrente , num ponto situado a uma distância do fio. Dê a resposta em função dos ângulos e formados entre a normal ao fio baixada do ponto e pelas retas que unem o ponto com as extremidades do fio considerado.
Ver solução completaQuestão 4
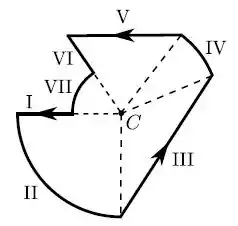
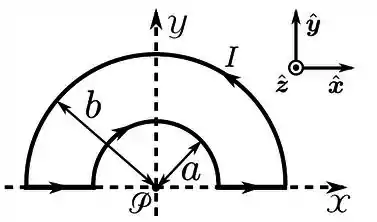
O fio que aparece na figura abaixo é percorrido por uma corrente . Qual é o valor da contribuição para o campo magnético no centro da semicircunferência devido
(a) a cada segmento retilíneo de comprimento ;
(b) à semicircunferência de raio ; e
(c) a todo fio?
Questão 5
Considere a espira da figura formada pelo arco de circunferência centrado em e raio , pelo segmento de comprimento sobre o eixo e pelo segmento paralelo ao eixo . A espira é percorrida por uma corrente de intensidade com sentido mostrado na figura (anti-horário).
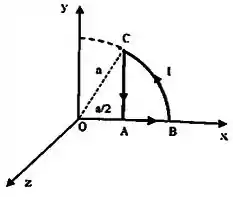
Nestas condições, utilizando explicitamente a Lei de Biot-Savart e justificando as suas afirmações, determine:
(a) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
(b) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
(c) O campo magnético (módulo, direção e sentido) na origem devido ao arco .
(d) O campo magnético total (módulo, direção e sentido) na origem .
Ver solução completaQuestão 6
Uma corrente estacionária, de intensidade , flui ao longo de um segmento retilíneo que se divide, igualmente, em quatro meridianos de uma esfera de raio , perpendiculares (dois a dois) entre si, e reencontrando-se num outro segmento retilíneo. Qual é o módulo do campo magnético no centro da esfera?
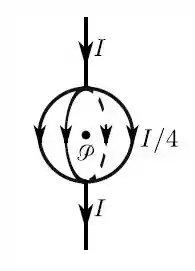
Questão 7
Dois fios muito longos são percorridos por correntes elétricas estacionárias de mesma intensidade. Cada um de tais fios é constituído por dois segmentos retilíneos (muito longos) e por um arco circular intermediário (com abertura de ); os raios de tais arcos são tais que . Qual dos segmentos dá maior contribuição para o campo magnético resultante no ponto central ?
- II
- V
- I e III
- IV e VI
- Todos contribuem igualmente para .
Questão 8
Calcule o campo magnético no ponto devido ao circuito com corrente estacionária de intensidade .
Questão 9
A Fig. 1 mostra um segmento retilíneo de comprimento de um fio que conduz corrente no sentido . O centro do segmento está na origem. Um ponto está sobre o eixo à distância da origem.
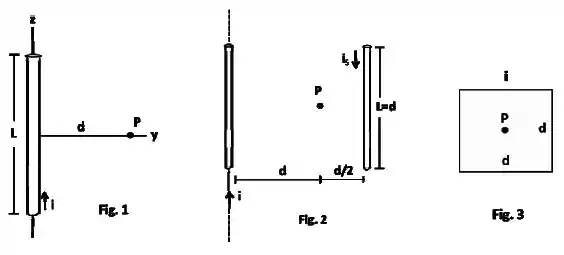
Mostre, utilizando explicitamente, a lei de Biot-Savart, que o vetor campo magnético em devido a todo o segmento é dado por:
Considere agora a Fig. 2 que mostra um ponto à distância de um fio infinito com corrente . O módulo do campo magnético devido ao fio infinito no ponto é dado por . A figura mostra também um segmento retilíneo com corrente antiparalela a . O segmento tem comprimento e está simetricamente disposto em relação ao ponto e dista dele.
Quanto deve valer a corrente para que o módulo do campo total em seja ?
Considere agora a Fig. 3 que mostra uma espira quadrada de lado que conduz uma corrente de valor . A espira é centrada em .
Utilizando o resultado do item , calcule o módulo do campo magnético em em função de , e . A corrente deve circular na espira no sentido horário ou anti-horário para que o campo em tenha sentido saindo da página?
Ver solução completaQuestão 10
O circuito da figura é formado por dois arcos de círculo de raios e e dois fios retilíneos de comprimento . Cada arco forma um setor de ângulo igual a . O circuito é percorrido por uma corrente de intensidade no sentido indicado. Calcule, justificando:
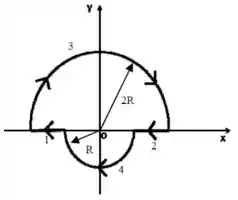
As contribuições e dos segmentos retilíneos, e
As contribuições e dos arcos de raio e
para o campo magnético (módulo, direção e sentido) na origem dos eixos , que corresponde ao centro dos dois arcos de círculo.
Considere agora que o arco de raio gire de em torno do eixo (= eixo de rotação).
Calcule os novos campos magnéticos e
Enfim, o circuito da figura acima é girado de um ângulo , conforme indica a Figura abaixo:
Calcule os novos campos magnéticos e .
Ver solução completaQuestão 11
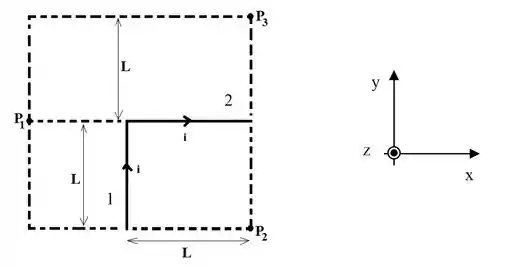
Um fio retilíneo de comprimento é percorrido por uma corrente como mostrado na figura ao lado (o sentido da corrente está indicado no desenho). O fio repousa sobre o eixo e suas extremidades estão nas coordenadas .
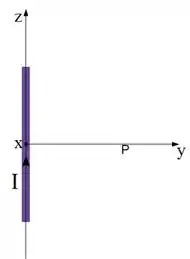
A partir da lei de Biot-Savart, encontre o vetor campo magnético no ponto mostrado na figura cuja coordenada é . (Considere
Partindo do resultado do item anterior, encontre o campo magnético para um fio muito longo .
Considere agora dois fios retilíneos muitos longos paralelos percorridos por correntes saindo e entrando no papel, respectivamente.
A partir do campo magnético encontrado no item , encontre o campo magnético resultante no ponto mostrado na figura.
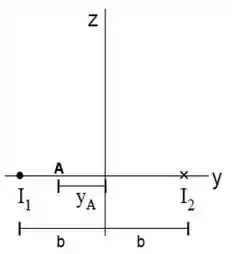
Questão 12
A figura mostra dois fios condutores de corrente. A corrente no fio tem o sentido positivo do eixo e a corrente no fio tem o sentido positivo do eixo . Com esta escolha de sistemas de coordenadas, o sentido positivo do eixo é para fora do papel. As corrente nos fios e são iguais a .
Utilizando explicitamente a lei de Biot-Savart:
Calcule o campo magnético gerado no ponto pela corrente no fio .
Calcule o campo magnético gerado no ponto pela corrente no fio
Calcule o campo magnético total gerado no ponto pelas correntes dos fios e .
Ver solução completaQuestão 13
Uma espira com corrente de intensidade tem a forma de dois arcos de circunferência concêntricos unidos por segmentos retilíneos. O arco de menor raio subentende um ângulo , e o raio do outro arco é . Os dois segmentos retilíneos são radiais em relação ao centro C da espira.
Adote o valor .
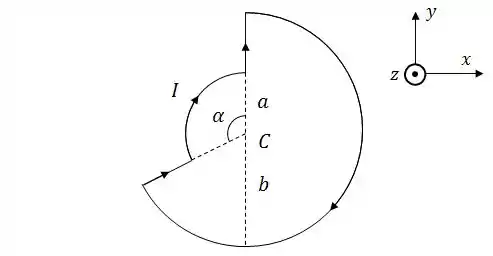
Usando a Lei de Biot-Savart e adotando o sistema de coordenadas da figura, calcule cada uma das contribuições para o vetor campo magnético gerado pela espira em seu centro :
contribuição dos segmentos retilíneos;
contribuição do arco menor;
contribuição do arco maior;
o vetor campo magnético total gerado pela espira em .
Sabendo que um campo magnético externo uniforme e muito intenso, dado por , está presente em toda a região da espira, calcule o vetor torque sobre a espira.
(Nota: use a aproximação ).
Considere agora uma nova situação na qual o campo magnético total em seja dado por , e que uma partícula de carga negativa de módulo passa por com velocidade . Calcule o vetor força magnética sobre a partícula.
Ver solução completaQuestão 14
Calcule o campo magnético no ponto devido ao circuito com corrente estacionária de intensidade .
Questão 15
Dois fios muito longos são percorridos por correntes elétricas estacionárias de mesma intensidade. Cada um de tais fios é constituído por dois segmentos retilíneos (muito longos) e por um arco circular intermediário (com abertura de ); os raios de tais arcos são tai que . Qual dos segmentos dá maior contribuição para o campo magnético resultante no ponto central ?
- II
- V
- I e III
- IV e VI
- Todos contribuem igualmente para .
Questão 16
Uma corrente estacionária, de intensidade , flui ao longo de um segmento retilíneo que se divide, igualmente, em quatro meridianos de uma esfera de raio , perpendiculares (dois a dois) entre si, e reencontrando-se num outro segmento retilíneo. Qual é o módulo do campo magnético no centro da esfera?
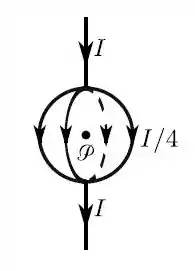
Questão 17
Considere uma espira quadrada de lado percorrida por uma corrente estacionária no sentido anti-horário, e sujeita a um campo magnético externo estacionário e uniforme . A espira se encontra no plano , conforme a figura.
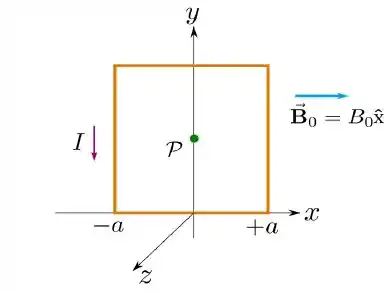
Calcule as forças sobre o lado horizontal superior do quadrado e sobre o lado vertical à direita do quadrado, exercidas pelo campo magnético externo.
Determine o momento de dipolo magnético associado à espira e calcule o vetor torque que o campo externo exerce sobre a mesma.
Determine o campo magnético produzido pela espira no seu centro .
Ver solução completaQuestão 18
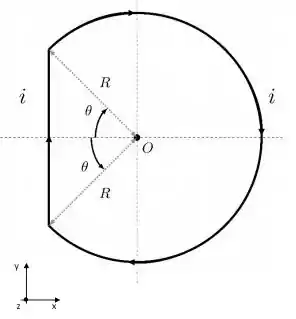
Um circuito é formado por duas semicircunferências de raios e , como é mostrado na figura abaixo.
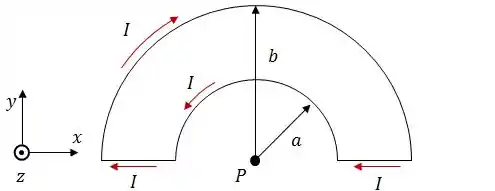
O vetor campo magnético produzido pelas correntes do fio no ponto P é dado por:
Ver solução completa
Questão 19
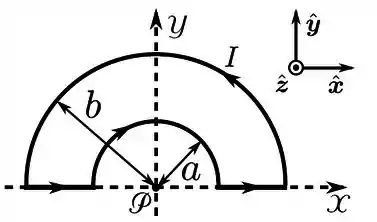
Uma corrente estacionária de intensidade percorre um circuito condutor que se encontra no plano de um sistema de coordenadas, como mostrado na figura abaixo. Esse circuito é formado por 3 arcos de circunferência idênticos de raio e ângulo central de , por outros 3 arcos de circunferência idênticos, de raio () e por segmentos de reta radiais que conectam os arcos, como indicado. Nessa situação, o campo magnético gerado por esse circuito no ponto vale:
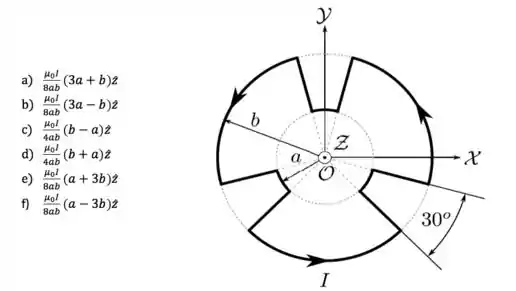
Questão 20
Uma corrente estacionária percorre o circuito condutor abaixo. Qual é o módulo do campo magnético no ponto ?
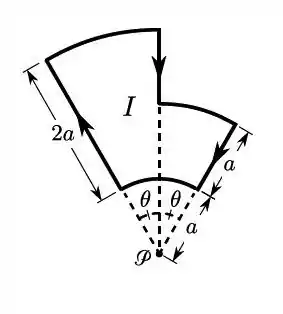
Questão 21
. Considere as representações e expressões para os seguintes campos vetoriais ( é uma constante positiva):
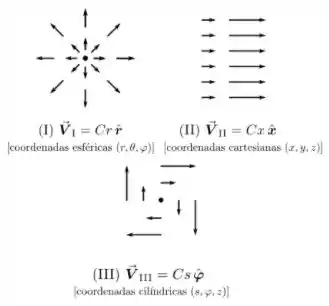
Qual(is) de tais campos nitidamente não pode(m) ser campo(s) magnético(s)?
Somente e
Somente e
Somente e
Nenhum deles pode ser campo magnético
Todos podem ser campos magnéticos
Somente
Somente
Somente
Ver solução completaQuestão 22
A figura abaixo mostra trechos de um fio condutor reto e uma fita condutora de comprimentos e , respectivamente. A fita possui largura e sua espessura pode ser desconsiderada. Correntes e percorrem o fio e a fita, respectivamente. A densidade linear de corrente na fita é uniforme .
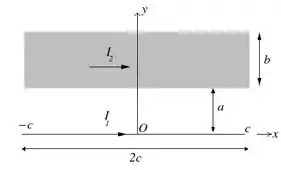
- Usando a Lei de Biot-Savart, calcule o vetor campo magnético produzido pelo fio num ponto situado ao longo do eixo .
- Considerando que agora o fio é infinito, , e a fita é infinita ao longo da direção , calcule o vetor força por unidade de comprimento produzida pelo fio sobre a fita.
Questão 23
Considere a figura a seguir, em que um arco de meia circunferência de raio porta uma corrente no sentido horário e a origem do sistema de coordenadas coincide com o centro do arco.
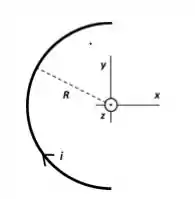
(a) Usando explicitamente a lei de Biot-Savart, calcule o vetor campo magnético (módulo, direção e sentido) produzido pelo arco na origem.
Sabemos que um fio retilíneo infinito que transporta uma corrente produz um campo magnético, a uma distância do fio, cujo módulo é dado por .
(b) Considere que o campo produzido na origem pelo arco da figura seja dado por .
Deseja-se posicionar um fio retilíneo infinito paralelo ao eixo de modo a anular o campo resultante na origem. Se o fio retilíneo porta uma corrente de no sentido , calcule a coordenada (incluindo o sinal) onde o fio deve ser posicionado.
(c) Partindo agora de uma situação em que o campo resultante é nulo na origem, encontre os dois únicos modos de posicionar um novo fio retilíneo de maneira a que o novo campo resultante possua somente componente . (Ou seja, encontre ao longo de qual direção e sentido deve estar a corrente do fio, e em que região do espaço ele deve ser posicionado).
Ver solução completaQuestão 24
A figura mostra três circuitos formados por dois segmentos radiais e dois arcos de circunferência concêntricos, um de raio e outro de raio . A corrente é a mesma nos três circuitos e o ângulos entre os dois segmentos radiais é o mesmo. Colocando os circuitos na ordem do módulo decrescente do campo magnético no centro dos arcos (marcado na figura por um ponto), obtemos
a) .
b) .
c) .
d) .
e) nenhuma das respostas está correta.
Ver solução completaQuestão 25
a) Um fio de comprimento infinito e raio desprezível transporta uma corrente . Utilize a lei de Biot-Savart e calcule o campo magnético a uma distância do fio.
b) Um fio, de raio desprezível, e que transporta uma corrente é configurado na forma de uma espira circular de raio . Utilize a lei de Biot-Savart e calcule o campo magnético no centro da espira.
Ver solução completaQuestão 26
Os dois fios retos, infinitos e paralelos ao eixo z têm raios a. Seus eixos, contidos no plano e também paralelos ao eixo, estão afastados conforme mostra a Figura. São percorridos por correntes iguais, uniformemente distribuídas nos seus interiores com densidade no sentido Determine o vetor campo magnético nos pontos:
- de coordenada .
- de coordenada .
- O vetor força (por unidade de comprimento) exercida pelo fio da esquerda sobre o fio da direita, de .
Em seguida, suponha que as correntes totais estejam concentradas nos respectivos eixos e determine:
Questão 27
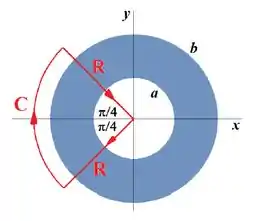
Um fio reto, infinito e oco (de raio interno e externo ) centrado no eixo tem a seção transversal (no plano mostrada na Figura. Este fio é percorrido por corrente com densidadeno sentido , onde . Determine:
- A corrente total em seção transversal arbitrária do fio.
- O vetor do campo magnético em um ponto arbitrário cuja distância ao eixo é
- O vetor do campo magnético em um ponto arbitrário cuja distância ao eixo é
- O vetor do campo magnético em um ponto arbitrário cuja distância ao eixo é
- O valor de ao longo do contorno orientado mostrado na figura, formado por duas radiais de comprimento e um quadrante de círculo de mesmo raio.
Questão 28
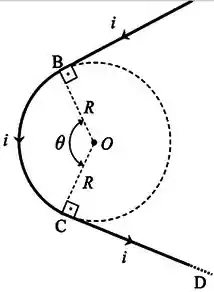
Na figura abaixo temos dois fios retilíneos semi-infinitos e , conectados a um fio curvo que é um segment circular de raio e abertura angular . Todos os fios pertencem ao plano da página e são percorridos por uma corrente elétrica constant . Nestas condições,
- Escreva a equação da lei de Biot-Savart em sua forma vetorial, identificando numa figura esquemática todos os elementos inerentes a tal equação
- Calcule o modulo do campo magnético total em , expressando seu resultado em termos de , e .
- Qual a direção e o sentido (com relação ao plano da página) do vetor campo magnético total em ?
Questão 29
A figura abaixo é composta por um fio, perpendicular ao plano da página, por onde passa uma corrente e por uma espira, no plano da página, com dois arcos de circunferência de raio e compreendidos entre um ângulo de .
Pela espira passa uma corrente de e o centro da mesma coincide com o fio no ponto .
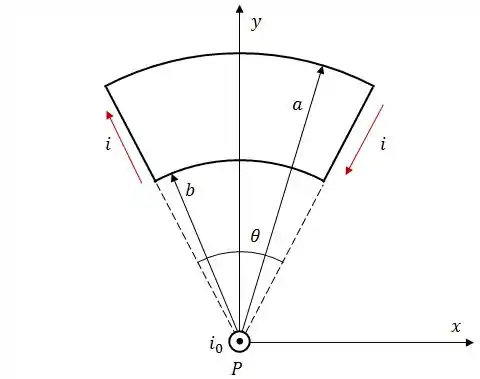
Determine:
O vetor momento de dipolo magnético da espira;
O vetor campo magnético no ponto ;
O torque que o campo do fio produz sobre a espira;
Ver solução completaQuestão 30
Um fio infinitamente longo transportando uma corrente é dobrado conforme a figura, sendo que a parte semicircular está contida no plano .
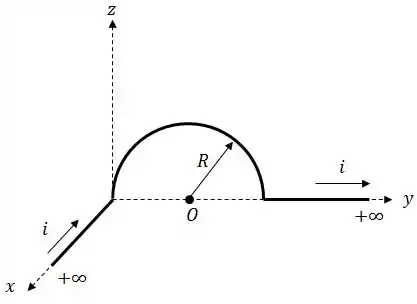
Calcule no ponto :
O vetor campo magnético devido às partes retas do fio;
O vetor campo magnético devido à espira semicircular;
O campo magnético total;
A força que atua sobre uma carga com velocidade no ponto ;
Ver solução completaQuestão 31
Uma espira condutora quadrada de lado transporta uma corrente estacionária de intensidade . Sobre o campo magnético produzido por essa espira, é CORRETO afirmar que:
- O campo magnético no centro da espira é nulo.
- O fluxo do campo magnético através da superfície plana definida pela área da espira é nulo.
- O campo magnético tem o mesmo módulo em todos os pontos sobre o eixo perpendicular ao plano da espira e que passa por seu centro.
- O módulo do campo magnético no centro da espira não depende do tamanho da mesma.
- Em pontos sobre o plano da espira, o campo magnético é perpendicular a este plano.
Questão 32
Considere um fio infinito formado por dois trechos retilíneos semi-infinitos e perpendiculares entre si, ligados por um arco de circunferência de raio R (um quarto de circunferência). Por esse fio flui uma corrente estacionária , como mostrado na Figura . Utilize o sistema de eixos cartesianos desenhado na Figura . Com essa escolha, um dos trechos retilı́neos é paralelo ao eixo , enquanto o outro é paralelo ao eixo , e o arco de circunferência tem centro na origem .
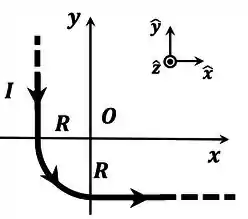
(a) Determine a contribuição ao campo magnético na origem do sistema de coordenadas indicado na Figura , devido ao trecho do fio correspondente ao arco de circunferência. Indique o módulo, a direção e o sentido de .
(b) Determine a contribuição ao campo magnético na origem do sistema de coordenadas indicado na Figura , devido ao trecho horizontal do fio. Indique o módulo, direção e sentido de .
(c) Determine o campo magnético (módulo, direção e sentido) produzido pelo fio completo, na origem do sistema de coordenadas.
Ver solução completaQuestão 33
Qual(is) afirmação(ões) é(são) correta(s) a respeito de forças e campos?
- As linhas de campo magnético de um fio com corrente saem radialmente.
- A energia cinética de uma partícula carregada pode ser aumentada pela ação de uma força magnética.
- Uma partícula carregada pode ser mover através de um campo magnético sem sentir uma força magnética.
- Somente III;
- Somente II;
- II e III;
- I e II;
- Nenhuma delas;
Questão 34
Considere o sistema na figura abaixo, formado por um fio infinito que, em um certo ponto, é enrolado formando uma espira circular de raio . Calcule o campo magnético no centro da espira.
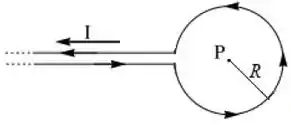
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 35
(I) (1,0 ponto) Uma espira plana, contida no plano , é constituída de um segmento circular de raio e dois segmentos retos de comprimento , conforme a figura. Pela espira flui o sentido anti-horário uma corrente . Calcule o vetor campo magnético produzido pela espira no ponto (origem do sistema de coordenadas).
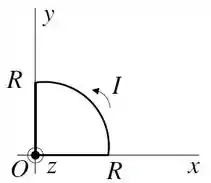
Questão 36
PARTE 1:
A figura abaixo mostra duas espiras planas: a espira 1 é circular, de raio ; a espira 2 é formada por duas semicircunferências, uma de raio e outra de raio , interligadas por dois segmentos retilíneos.
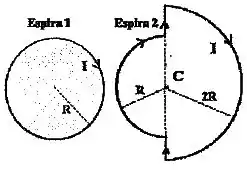
Correntes de mesma intensidade circulam pelas duas espiras.
Seja o módulo do campo magnético gerado pela espira 1 em seu centro, e o módulo do campo magnético gerado pela espira 2 em seu centro (ponto C). Considerando que as espiras estão muito afastadas uma da outra, calcule a razão .
Ver solução completaQuestão 37
Considere um fio de comprimento por onde passa uma corrente colocado ao longo do eixo , conforme a figura.
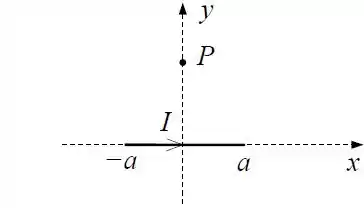
Usando a lei de Biot-Savart, calcule o campo magnético num ponto do eixo .
Calcule o campo magnético no limite em que .
Ver solução completaQuestão 38
Considere uma espira retangular de lados e () e um fio retilíneo infinito, no mesmo plano da espira. Sabendo que o fio retilíneo é paralelo aos lados longos da espira e que o fio e a espira portam, respectivamente, correntes estacionárias para a direita e no sentido horário, assinale a única opção INCORRETA.
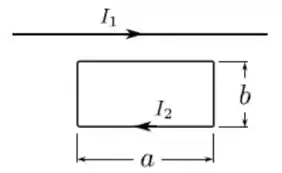
- A força sobre cada um dos lados curtos da espira é não-nula.
- A soma vetorial das forças sobre os lados curtos da espira é nula.
- A soma vetorial das forças sobre os lados longos da espira é nula.
- As forças sobre os lados longos da espira estão na mesma direção.
- A força resultante sobre a espira tem direção perpendicular ao fio retilíneo.
Questão 39
Duas espiras condutoras circulares, concêntricas, encontram-se sobre um mesmo plano. A primeira espira tem raio e transporta uma corrente estacionária de intensidade . A segunda tem raio e também transporta uma corrente estacionária em sentido oposto ao da primeira. Sabendo que o campo magnético produzido pelas duas espiras é nulo no centro delas, a intensidade da corrente na segunda espira vale:
Questão 40
Um anel fino de raio , carregado com densidade linear de carga , gira em torno de um eixo que passa pelo centro com uma velocidade angular , conforme a figura.
Atua na região um campo magnético externo homogêneo .
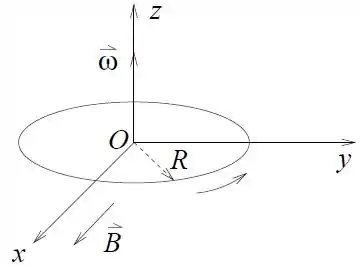
- Calcule a corrente associada ao movimento do anel em função de , e . Qual é o sentido da corrente?
- Calcule o vetor torque que o campo externo exerce sobre o anel.
- Calcule o campo magnético produzido pelo anel no seu centro.
Questão 41
Duas partículas 1 e 2, carregadas positivamente, estão se movendo num mesmo plano, com a velocidade da partícula 1 sendo perpendicular à velocidade da partícula 2. No instante mostrado na figura, a partícula 2 está sobre a reta que define a direção da velocidade da partícula 1. Sejam a força exercida sobre a partícula 1 e a força exercida sobre a partícula 2. Para esse instante, a orientação da força magnética que cada partícula exerce sobre a outra é:
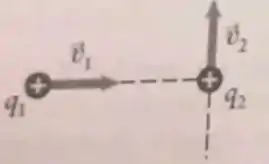
- para cima no plano da página;
- , para baixo no plano da página;
- , para cima no plano da página;
- , para baixo no plano da página;
- , para baixo no plano da página;
Questão 42
Um fio fino, retilíneo, de comprimento , transporta uma corrente estacionária de intensidade , suprida por uma bateria. Considere um ponto sobre um eixo perpendicular ao fio e que passa por seu centro, a uma distância do mesmo. Se este ponto se encontra muito próximo do centro do fio, de forma que , podemos afirmar que a intensidade do campo magnético produzido pelo fio neste ponto será proporcional, aproximadamente, a:
Questão 43
Uma espira condutora circular de raio é posicionada sobre o plano de um sistema de coordenadas com seu centro sobre a origem, como mostrado no lado esquerdo da figura abaixo. Ela transporta uma corrente estacionária de intensidade , no sentido indicado.
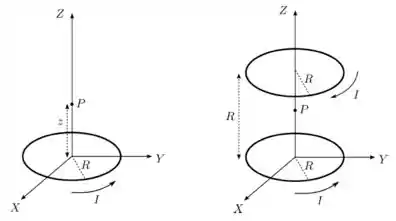
- Utilizando a lei de Biot-Savart, determine o campo magnético produzido pela espira (módulo, direção e sentido) em um ponto localizado sobre o eixo .
- Uma segunda espira, idêntica à primeira, é posicionada paralelamente ao plano com centro no ponto . Ela transporta uma corrente estacionária de mesma intensidade , mas em sentido oposto ao da primeira, como indicado no lado direito da figura. Determine o campo magnético total (módulo, direção e sentido) produzido pelas duas espiras no mesmo ponto .
- Determine o campo magnético total quando .
Questão 44
Considere uma espira quadrada de lado percorrida por uma corrente . A espira se encontra no plano , conforme a figura.
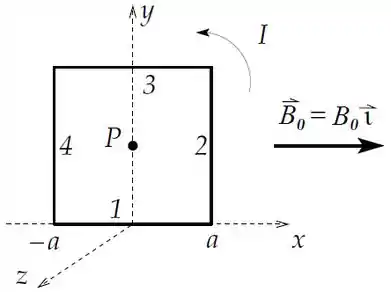
Determine o campo magnético produzido pela espira no seu centro .
Sugestão: Calcule o campo produzido pelo lado e use a simetria do problema.
Ver solução completaQuestão 45
Considere um sistema formado por um fio fino, retilíneo e infinito coplanar a uma espira circular, como mostrado na figura abaixo. Tanto o fio retilíneo quando a espira circular transportam correntes estacionárias de intensidade , com os sentidos indicados na figura. Nessa situação, podemos afirmar que o sentido das forças que o fio exerce sobre a espira, e que a espira exerce sobre o fio são, respectivamente:
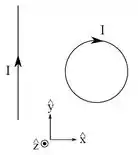
- Não haverá força resultante sobre o fio e a espira.
Questão 46
Um fio condutor fino é formado pela junção de dois trechos semicirculares de raios e com dois trechos retilíneos, como mostrado na figura abaixo. Uma corrente estacionária de intensidade percorre o condutor no sentido indicado (anti-horário no semicírculo menor). Nessa situação, qual é o campo magnético resultante produzido pelo fio no centro dos semicírculos (ponto )?
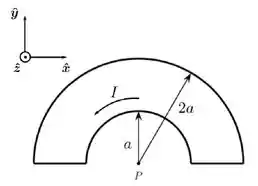
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 47
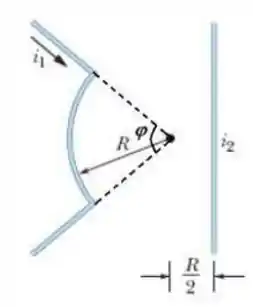
A figura abaixo mostra dois fios. O fio é formado por um arco de circunferência de raio e dois segmentos radiais que conduz uma corrente no sentido indicado. O fio é muito longo e retilíneo, conduz uma corrente que pode ser ajustada e está a uma distância do centro do arco. O campo magnético produzido pelas duas correntes é medido no centro de curvatura do arco. Determine o ângulo , em graus, subtendido pelo arco e o sentido da corrente para que o valor do campo magnético no centro do arco seja nulo. Use a Lei de Biot-Savart para o fio e a Lei de Ampére para o fio .
Questão 48
Um circuito no plano formado por uma semicircunferência de raio com centro de curvatura na origem e um trecho reto ao longo do eixo é preenchido por uma corrente no sentido indicado na figura.
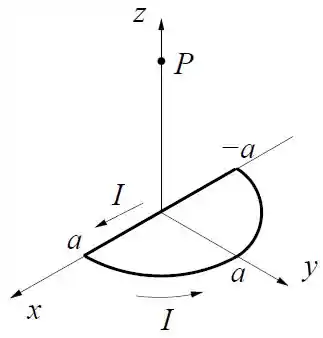
Dado: O elemento de linha infinitesimal de semicircunferência é , onde o ângulo é medido a partir do eixo .
- Calcule o vetor campo magnético produzido pelo trecho reto no ponto .
- Calcule o vetor campo magnético produzido pelo trecho de semicircunferência no ponto .
Questão 49
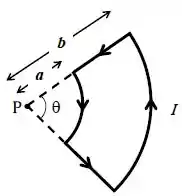
Considere o circuito da figura, por onde circula uma corrente . Os segmentos curvos são arcos de círculos com raios e e ângulo . Os segmentos retos estão dispostos ao longo dos raios.
- Use a lei de Biot-Savart para encontrar a expressão literal para o campo magnético no ponto . Substitua os valores e indique o valor do módulo do campo.
Questão 50
2 - Sabemos que um capacitor de placas paralelas (com o diâmetro das placas muito maior que a distância entre elas) possui a propriedade de confinar o campo elétrico em seu interior. Essa propriedade se generaliza para capacitores das mais variadas formas. Da mesma maneira, podemos pensar em sistemas magnéticos análogos ao capacitor (sistemas que possuem campo magnético confinado ao interior de uma determinada região). Pensando nisso, considere os quatro sistemas abaixo:
I - Solenoide infinito (comprimento do solenoide muito maior que seu raio) com corrente .
II - Solenoide finito (comprimento do solenoide da mesma ordem de grandeza que seu raio) com corrente I.
III - Cabo coaxial com correntes I e -I (sentidos opostos).
IV - Cabo coaxial com correntes I e I (mesmo sentido).
- Apenas I e III representam sistemas que confinam campo magnético em seus interiores.
- Os sistemas I e III confinam o campo magnético em seus interiores, enquanto nos sistemas II e IV o campo magnético confinado é nulo.
- Todos os sistemas (I, II, III e IV) confinam o campo magnético em seus interiores.
- Os sistemas II e IV confinam o campo magnético em seus interiores, enquanto nos sistemas I e III o campo magnético confinado é nulo.
- Apenas II e IV representam sistemas que confinam campo magnético em seus interiores.
Questão 51
12 - Ainda sobre o circuito da questão anterior (reproduzido aqui), o vetor que melhor descreve o campo magnético no ponto C é:
![]()
Questão 52
. Uma espira condutora circular de raio é posicionada sobre o plano de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ela transporta uma corrente estacionária de intensidade , no sentido indicado. Considere um elemento de comprimento infinitesimal desta espira, localizado no ponto e orientado no sentido da corrente. Qual é o campo magnético produzido por este elemento em um ponto localizado sobre o eixo ?
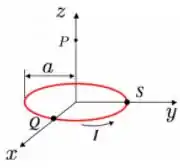
Escolha uma opção:
Ver solução completaQuestão 53
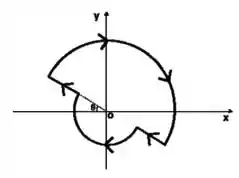
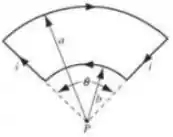
Considere o circuito da figura abaixo, composto por dois lados retilíneos e dois arcos de círculo, ambos definidos por um ângulo .
O menor arco está a uma distância do ponto e o maior a uma distância do mesmo ponto . O circuito é percorrido por uma corrente no sentido anti-horário.
Assinale a opção que especifica corretamente o vetor campo magnético resultante em .
, perpendicular ao plano da página e entrando na página.
, perpendicular ao plano da página e entrando na página.
, perpendicular ao plano da página e entrando na página.
, perpendicular ao plano da página e saindo da página.
, perpendicular ao plano da página e saindo da página.
Ver solução completaQuestão 54
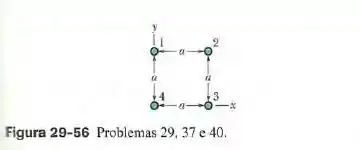
(Capítulo 29.3 – Exercício 37) Na figura 29-56, quatro fios retilíneos são perpendiculares ao papel e suas seções retas formam um quadrado de aldo . Todos os fios conduzem correntes de e as correntes são para fora do papel nos fios 1 e 4 e para dentro do papel nos fios 2 e 3. Em termos dos vetores unitários, qual é a força magnética por metro de fio que age sobre o fio 4?
Questão 55
A figura abaixo mostra um cilindro condutor muito longo de raio 𝑎, que possui uma densidade de corrente , e está circundado por uma camada cilíndrica condutora, de raio interno 𝑎 e raio externo 𝑏, que possui uma densidade de corrente , no sentido oposto da corrente do cilindro interno.
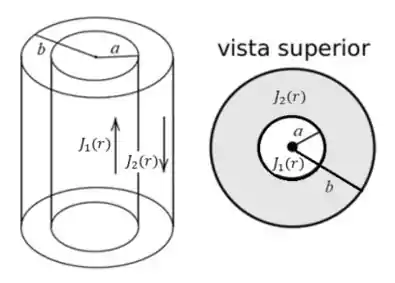
i. Usem os 2 últimos dígitos dos seus RAs (considerem que estes formam um único número de 2 dígitos; p. ex., se o RA é 123456, o número a ser usado será 56), para calcular o valor do parâmetro :
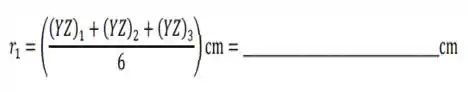
ii. Usem os 2 dígitos do meio dos seus RAs (considerem que estes formam um único número de 2 dígitos; p. ex., se o RA é 123456, o número a ser usado será 34), para calcular o valor do parâmetro :
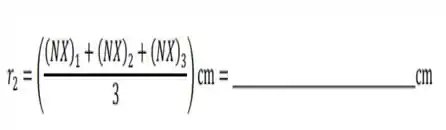
Usem o menor valor dentre e para ser o valor de 𝑎 e o maior para ser o valor de 𝑏. Caso , façam e (p. ex., se e , então e ; e caso , então e ).
iii. Usem os últimos dígitos dos seus RAs (p. ex., se o RA é 123456, o número a ser usado será 6) para obter:

iv. Usem os penúltimos dígitos dos seus RAs (p. ex., se o RA é 123456, o número a ser usado será 5) para calcular para calcular o parâmetro :
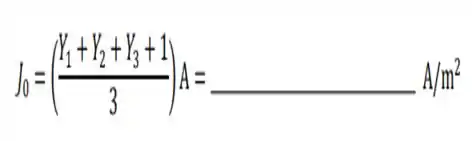
Resolvam os itens a seguir. Se necessário, usem . Não se esqueçam de detalhar todos os desenvolvimentos e não pular passagens.
a) Encontrem uma expressão algébrica para o módulo do campo magnético a uma distância 𝑟 do eixo do conjunto cilíndrico para . Depois, calculem o módulo do campo magnético para .
b) Encontrem uma expressão algébrica para o módulo do campo magnético a uma distância 𝑟 do eixo do conjunto cilíndrico para . Depois, calculem o módulo do campo magnético para .
c) Encontrem uma expressão algébrica para o módulo do campo magnético a uma distância 𝑟 do eixo do conjunto cilíndrico para . Depois, calculem o módulo do campo magnético para .
d) Há valores finitos de 𝑟 para os quais o campo magnético é zero? Se sim, quais? Justifiquem! Encontrem primeiro a expressão algébrica, e depois substituam os valores
Ver solução completaQuestão 56
Uma espira condutora circular de raio é posicionada sobre o plano de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ela transporta uma corrente estacionária de intensidade , no sentido indicado. Considere um elemento de comprimento infinitesimal desta espira, como indicado na figura. Qual é a componente radial (perpendicular ao eixo ) da contribuição deste elemento para o campo magnético em um ponto localizado sobre o eixo ?
Escolha uma:
Ver solução completaQuestão 57
A figura ao lado representa uma espira composta por uma seção incompleta de circunferência de raio , cujas extremidades são unidas por um segmento reto. A espira é percorrida por uma corrente i constante e uniforme, cujo sentido está representado na Figura através das setas. Sabendo que o ângulo e utilizando explicitamente a lei de Biot-Savart, calcule:
a) O vetor campo magnético gerado pela seção incompleta de circunferência no ponto O.
b) O vetor campo magnético gerado pela seção reta no ponto O.
Ver solução completaQuestão 58
Considere o circuito da figura abaixo, constituído por segmentos retilíneos (I, III, V e VI) e segmentos de arco de círculos (II, IV e VII) concêntricos com o ponto , percorridos por uma corrente estacionária , com sentido assinalado. Indique quais de tais segmentos dão uma contribuição não nula para o campo magnético resultante no ponto .
- II, III, IV, V e VII
- I, III, V e VI
- II, IV e VII
- I, II, IV, VI e VII
- Todos criam campo magnético não nulo em
Questão 59
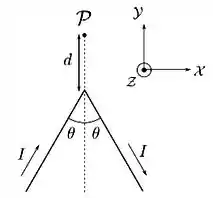
Um fio condutor fino, retilíneo e infinito é dobrado de forma que suas duas metades formam um ângulo entre si, como mostrado na figura abaixo. O fio é atravessado por uma corrente estacionária de intensidade no sentido indicado. Utilizando a lei de Biot-Savart e o sistema de coordenadas indicado na figura, determine o campo magnético (módulo, direção e sentido) no ponto mostrado na figura, localizado a uma distância do ponto de dobra, ao longo da reta bissetriz do ângulo . Analise e interprete o caso limite .
Questão 60
i. Considere uma espira quadrada de lado percorrida no sentido anti-horário por uma corrente . A espira se encontra no plano , conforme a figura.
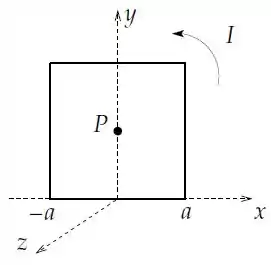
(a) Calcule o vetor campo magnético produzido pelo segmento da espira ao longo do eixo no centro da espira (ponto ).
(b) Calcule o vetor campo magnético total produzido pelos quatro segmentos no centro da espira.
Ver solução completaQuestão 61
Considere a espira da figura formada pelo arco de circunferência centrado em e raio , pelo segmento de comprimento sobre o eixo e pelo segmento paralelo ao eixo . A espira é percorrida por uma corrente de intensidade com sentido mostrado na figura (anti-horário).
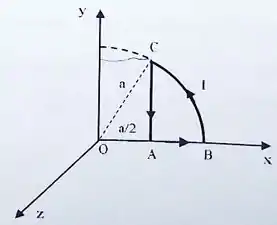
Nestas condições, utilizando explicitamente a Lei de Biot-Savart e justificando as suas afirmações, determine:
(a) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
(b) O campo magnético (módulo, direção e sentido) na origem devido ao segmento .
(c) O campo magnético (módulo, direção e sentido) na origem devido ao arco .
(d) O campo magnético total (módulo, direção e sentido) na origem .
Ver solução completaQuestão 62
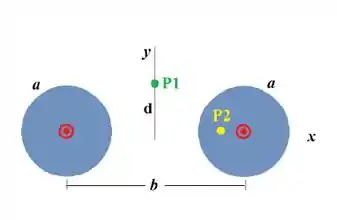
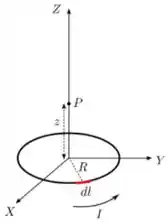
Um anel circular, de raio , situado no plano , com centro na origem, transporta uma corrente elétrica estacionária de intensidade e sentido indicado, como mostrado no lado esquerdo (a) da figura abaixo.
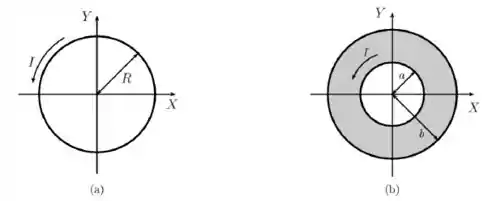
- Utilizando a lei de Biot-Savart, determine o campo magnético (módulo, direção e sentido) produzido pelo anel na origem
Considere, agora, uma coroa circular condutora, de raios interno e externo , também situada no plano e com centro na origem, transportando uma corrente elétrica estacionária de intensidade , uniformemente distribuída através de sua superfície, como mostrado no lado direito (b) da mesma figura.
b) Determine o campo magnético (módulo, direção e sentido) produzido pela coroa na origem. Sugestão: imagine a coroa como vários anéis concêntricos de raio e largura infinitesimal , através dos quais passa uma corrente de intensidade
Ver solução completaQuestão 63
Considere o circuito da figura, por onde circula uma corrente . Os segmentos curvos são arcos de círculos com raios e e ângulo . Os segmentos retos estão dispostos ao longo dos raios.
- Use a lei de Biot-Savart para encontrar a expressão literal para o campo magnético no ponto . Substitua os valores e indique o valor do módulo do campo.
- Indique a direção e sentido do campo magnético.
Questão 64
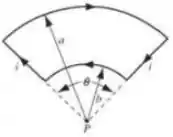
Considere os dois fios condutores mostrados na figura abaixo. Um deles é retilíneo e infinito, enquanto o outro é retilíneo e infinito, exceto por uma parte dobrada na forma de um semicírculo de raio .
Os fios carregam correntes estacionárias de intensidades e no mesmo sentido, respectivamente, e a distância entre eles também vale . Qual deve ser a razão para que o campo magnético no centro do semicírculo seja nulo?
;
;
;
;
;
O campo nunca pode ser nulo neste ponto, pois as correntes tem o mesmo sentido.
Ver solução completaQuestão 65
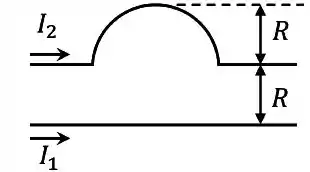
(Capítulo 29.3 – Exercício 41) Na figura 29-65, um fio retílíneo longo conduz uma corrente e uma espira retangular conduz uma corrente . Suponha que , e . Em termos dos vetores unitários, qual é a força a que está submetida a espira?
Questão 66
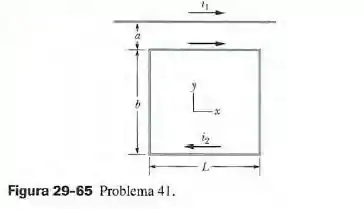
(Capítulo 29.3 – Exercício 39) Na figura 29-63, cinco fios paralelos longos no plano estão separados por uam distância . As correntes para dentro do papel são , , e ; a corrente para fora do papel é . Qual é o módulo da força por unidade de comprimento que age sobre o fio 3?
Questão 67
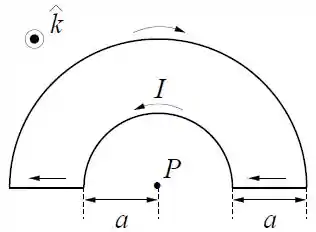
A figura abaixo mostra um circuito formado por dois trechos semicirculares de raios e e dois trechos retos. Uma corrente percorre o circuito no sentido indicado na figura. Calcule o campo magnético no ponto .
Questão 68
1 – a) Mostre com argumentos de simetria, que o campo magnético gerado pela densidade de corrente , com constantes e , gera um campo magnético que tem forma . Mostre também que é uma função ímpar, isto é . b) Calcule o campo .
Ver solução completaQuestão 69
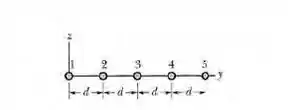
(Capítulo 29.3 – Exercício 36) Na figura 29-63, cinco fios paralelos longos no plano estão separados por uma distância , têm de comprimento e conduzem correntes iguais de para fora do papel. Em termos dos vetores unitários, determine a força (a) sobre o fio 1. (b) sobre o fio 2; (c) sobre o fio 3; (d) sobre o fio 4; (e) sobre o fio 5.
Questão 70
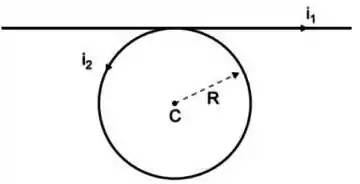
Na figura estão representados um fio muito longo percorrido por uma corrente e uma espira circular de raio , percorrida pela corrente , ambos num mesmo plano e um tangenciando o outro, conforme a figura. Qual é o valor da razão para que o campo magnético resultante no centro da espira seja nulo)
Questão 71
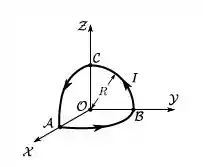
Um circuito fino, percorrido por uma corrente estacionária de intensidade , é constituído por 3 quartos de circunferência. Todos esses 3 arcos têm raio e situam-se em 3 diferentes planos ortogonais, com centro comum com a origem O de um sistema de coordenadas cartesianas, conforme mostra a figura abaixo. Qual é o campo magnético produzido por este circuito na origem O?
Questão 72
Determine o módulo, a direção e o sentido do campo magnético resultante no ponto da figura abaixo, que representa dois fios finos isolados conduzindo corrente . Considere o ponto localizado no centro das duas semi-circunferências e na direção dos fios retilíneos
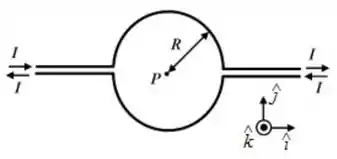
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 73
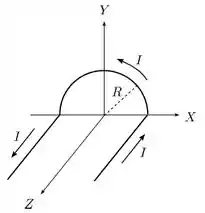
O fio condutor fino mostrado na figura abaixo é formado por dois trechos retilíneos e
semi-infinitos, paralelos ao eixo de um sistema de coordenadas, unidos por um trecho semicircular de raio contido no plano e centrado na origem. Este fio transporta uma corrente estacionária de intensidade , no sentido indicado na figura. Nessa situação, determine, justificando cuidadosamente todo o desenvolvimento:
(a) O vetor campo magnético resultante produzido pelos dois trechos retilíneos na origem.
(b) O vetor campo magnético produzido pelo trecho semicircular na origem.
(c) O vetor campo magnético resultante produzido pelo fio na origem e o módulo deste campo.
Questão 74
. Considere a espira condutora mostrada na figura abaixo. Ela é formada pela junção de dois trechos semicirculares de raios e com dois trechos retilíneos e conduz uma corrente estacionária de intensidade no sentido indicado.
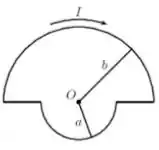
Deduza, em detalhe, uma expressão para o vetor campo magnético produzido pela espira
no ponto , que corresponde ao centro comum dos trechos semicirculares.
Ver solução completaQuestão 75
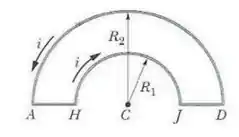
11 - O circuito ao lado transporta uma corrente . Considere as seguintes afirmações:
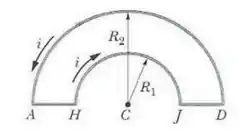
(I) As porções AH e JD não contribuem para o campo magnético produzido no ponto C.
(II) As porções semicirculares HJ e DA não contribuem para o campo magnético produzido no ponto C.
(III) A maior contribuição para o campo magnético produzido no ponto C vem da porção semicircular DA.
(IV) A maior contribuição para o campo magnético produzido no ponto C vem da porção semicircular HJ.
Destas quatro afirmações, as corretas são:
- (I) e (III).
- Todas.
- Nenhuma.
- (I) e (IV).
- (I), (II) e (IV).
Questão 76
O arranjo ilustrado na figura abaixo é composto por seis fios retilíneos finitos de comprimento . A corrente elétrica que circula em tal arranjo é . Usando a lei de Biot-Savart, calcule:
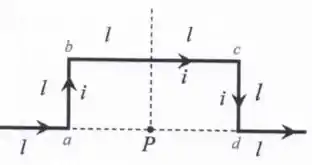
- O módulo do campo magnético no ponto devido ao fio localizado ao longo do segmento .
- O módulo do campo magnético no ponto devido aos fios localizados ao longo do segmento .
- O módulo, direção e sentido do campo magnético total no ponto .
Questão 77
Um resistor circular de raio contido no plano e centrado na origem é feito de duas metades com resistências e . O resistor está ligado a um par de fios semi-infinitos que se estendem ao longo do eixo e que são percorridos por uma corrente , conforme a figura.
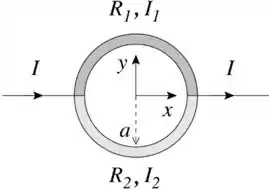
(a) Calcule o valor das correntes e que atravessam respectivamente os resistores e em função de , e . Indique o sentido de cada uma das correntes.
(b) Calcule o vetor campo magnético no centro do resistor circular.
Ver solução completa