Em uma certa região existe uma densidade de corrente uniforme de no sentido positivo do eixo . Determine o valor de quando a integral de linha é calculada ao longo de três segmentos de reta, de para , para para, com

A lei de Àmpere é utilizada para determinar o campo magnético total de uma região que apresente algum tipo de simetria. De acordo com ela:

O círculo do sinal de integral indica que a integração do produto escalar deve ser realizada para uma curva fecahda, conhecida como amperiana. A corrente é a corrente total envolvida pela curva fechada. Essa corrente tamém pode ser escrita como:

,

onde é a densidade de corrente na curva fechada.

No nosso exercício, vamos desenhar a região primeiro.

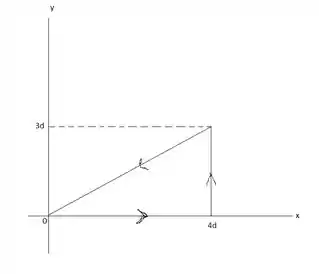
A área envolvida pela integral é um triângulo! A área de um triângulo nós sabemos lá da geometria plana, que é base vezes a altura, divido por 2. Assim,