Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.Problemas Adicionais - Ex. 64
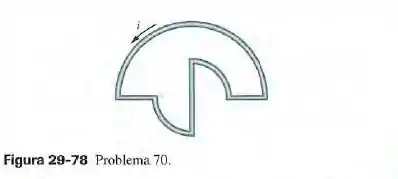
A figura 29-78 mostra uma espira percorrida por uma corrente . A espira é formada por uma semicircunferência de de raio, dois quartos de circunferência dede raio cada um e três segmentos retilíneos. Qual é o módulo do campo magnético no centro comum dos arcos de circunferência?
Passo 1
Bom, lá da teoria de campos magnéticos produzidos por correntes, temos a situação de um campo produzido no centro de um arco de circunferência, lembra? Lá a gente encontra a seguinte fórmula para calcular o campo:
Os segmentos retilíneos não contribuem para o campo , uma vez que o ângulo deles em relação ao ponto onde que remos calcular o campo magnético é .
Passo 2
Chamando de a direção para fora do papel, a contribuição dos arcos de circunferência é dada pela expressão a seguir:
Isso nos dá .
Resposta
O módulo do campo magnético é: