Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.Problemas Adicionais - Ex. 90a
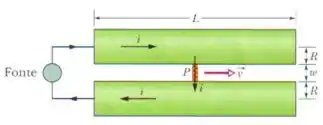
A figura 29-88 é um desenho esquemático de um canhão de elétromagnético. O projétil é colocado entre dois trilhos de seção reta circular, uma fonte faz passar uma corrente nos tribos e no projétil, que é feito de material condutor (não é necessário usar um fusível). (a) Seja a distância entre os trilhos, o raio dos trilhos e a corrente. Mostre que o projétil é submetido a uma força para a direita, paralela aos trilhos, cujo módulo é dado aproximadamente por:
Passo 1
Fala aí! tudo certinho? 😁
Nesse problema temos um canhão eletromagnético e nosso objetivo é mostrar que a força que o projetil é submetido tem módulo.
Tem ideia de como fazemos isso? 🤔
Considere um segmento do projétil entre e . Podemos usar a equação do campo magnético para fio retilíneo semi-infinito para calcular o campo magnético produzido pelos trilhos, considerados como fios sem-infinitos, chamando o trilho de cima de 1 e o trilho de baixo de 2, e a equação de força entre dois condutores paralelos para calcular a força magnética que age sobre o segmento.
Tranquilo até aqui? 😎
Passo 2
A corrente no trilho 1 é no sentido e a corrente no trilho 2 é no sentido.
Na região entre os fios, os campos têm o mesmo sentido, o sentido (para dentro do papel), e a força que age sobre o segmento do projétil é:
A força que age sobre o projétil é, portanto:
E aí! legal, né? Responde Aí! 😉
