Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.Problemas Adicionais - Ex. 77

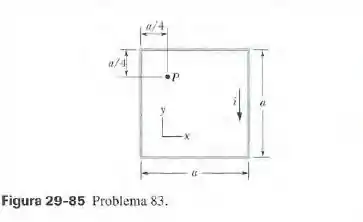
Em termos dos vetores unitários, qual é o campo magnético no ponto P da figura 29-85 se i = 10   A e a = 8,0   c m ? (observe que os fios não são longos)

Passo 1

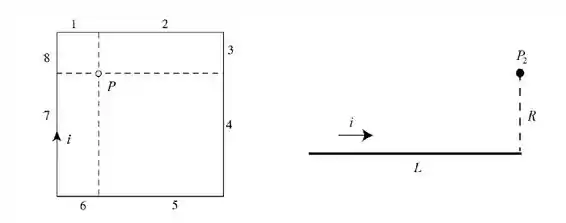
Para resolver essa questão podemos começar dividindo o quadrado da figura 29-85 nos segmentos numerados de 1 a 8 na figura a seguir, à esquerda, todos os quais podem ser considerados variações da siatuação mostrada na figura da direita.

Passo 2

Vamos assumir que o eixo x coincide com o fio, com a origem na extremidade direta, e supor que o sentido da corrente é o sentido positivo do eixo x . Todos os segmentos do rio produzem campos magnéticos no ponto P 2 orientado para fora do papel. De acordo com a lei de Biot-Savart, o módulo do campo produzido por um segmento infinitesimal do fio no ponto P 2 é dado por:

d B = μ o i 4 π ⋅ s e n θ r 2 d x ,

Na qual θ (o ângulo entre o segmento e a reta que liga o segmento a P 2 ) e r (o comprimento da reta) são funções de x . Substituindo r por x 2 + R 2 , s e n θ por R r = R x 2 + R 2   e integrando de x = - L   a x = 0 , obtemos:

B = μ o i R 4 π ∫ - L 0 d x x 2 + R 2 3 2 = μ o i R 4 π * 1 R 2 ⋅ x x 2 + R 2 3 2 - L 0 B = μ o i 4 π R ⋅ L L 2 + R 2

Agora, os campos magnétios produzidos pelos 8 segmentos são:

B P 1 = B P 8 = 2 μ o i 8 π a 4 = 2 μ o i 2 π a B P 4 = B P 5 = 2 μ o i 8 π 3 a 4 = 2 μ o i 6 π a B P 2 = B P 7 = μ o i 4 π a 4 ⋅ 3 a 4 3 a 4 2 + a 4 2 = 3 μ o i 10 π a B P 3 = B P 6 = μ o i 4 π 3 a 4 ⋅ a 4 3 a 4 2 + a 4 2 = μ o i 3 10 π a

Passo 3

Somando todas as contribuições, obtemos:

B P → = ∑ n = 1 8 B P n - k ^ = - 2 μ o i π a 2 2 + 2 6 + 3 10 + 1 3 10 k ^

B P → = - 2 4 π × 10 - 7   T . m A π 8,0 × 10 - 2   m 2 2 + 2 6 + 3 10 + 1 3 10 k ^

B P → = - 2,0 × 10 - 4   T k ^ = ( - 0,20   m T ) k ^

no qual k ^ é um vetor unitário que aponta para fora do papel.

Resposta

O campo magnético no ponto P é:

B P → = ( - 0,20   m T ) k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura 29-81 mostra, em seção reta, dois fios longos paralelos separados por uma distância d = 10c m ; os dois fios conduzem uma corrente de 100A , que tem o sentido para fora do papel no fio 1. O p
Um fio longo vertical conduz uma corrente desconhecida. Um cilindro oco, longo, de espessura desprezível, coaxial com o fio conduz uma corrente de 30m A , dirigida para cima; A superfície do cilindro
Um fio nu de cobre calibre 10 (ou seja, com 2,6m m de diâmetro) pode conduzir uma corrente de 50A sem superaquecer. Para essa corrente, qual é o módulo do campo magnético na superfície do fio?
O módulo do campo magnético a 88,0c m do eixo de um fio retilíneo longo é 7,30μ T . Determine a corrente no fio.
Três fios longos são paralelos ao eixo z e conduzem uam corrente de 10A no sentido positivo do eixo z . Os pontos de interseção dos fios com o plano x y formam um triângulo equilátero com 10c m de lad