Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.Problemas Adicionais - Ex. 96
A figura mostra uma barra de comprimento formada por dois materiais. O trecho de comprimento é feito de um material com um coeficiente de dilatação linear ; o trecho de comprimento é feito de um material com um coeficiente de dilatação linear . (a) Qual é o coeficiente de dilatação da barra como um todo? Se , o material é aço, o material é latão e , qual é o valor (b) de e (c) de ?
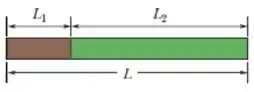
Passo 1
(a) Vamos começar encontrando o coeficiente de dilatação linear da barra inteira em função dos coeficientes das suas duas partes.
Precisamos de uma expressão para a variação do comprimento da barra inteira:
Ao mesmo tempo, se conhecêssemos o coeficiente de dilatação linear da barra, poderíamos escrever:
Vamos igualar as duas expressões:
Passo 2
Podemos consultar uma tabela para ver que:
E se subtituirmos esses e os outros valores na expressão que acabamos de encontrar, teremos o seguinte:
Nosso objetivo é determinar e , ou seja, duas variáveis. Isso quer dizer que vamos precisar de duas equações.
A segunda equação pode ser determinada lembrando que :
Então:
Simplificando um pouco:
Passo 3
(b) Vamos resolver esse sistema. Podemos isolar na primeira equação e substituir na segunda:
Passo 4
(c) Agora podemos substituir na segunda equação para calcular :
Resposta
(a) .
(b) .
(c) .