Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.Problemas Adicionais - Ex. 95
Uma onda progressiva de amplitude incide em uma interface. A onda refletida, de amplitude menor , se combina com a onda incidente. A figura de interferência resultante é mostrada na figura. A relação de onda estacionára é definida pela equação:
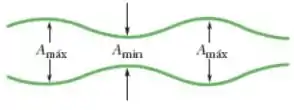
O coeficiente de reflexão é a razão entre a potência da onda refletida e a potência da onda incidente, o que significa que é proporcional a . Qual é o valor de (a) para reflexão total e (b) para reflexão nula? (c) Qual é o coeficiente de reflexão, em termos percentuais, para ?
Passo 1
(a) Nosso primeiro objetivo é calcular para o caso de reflexão total.
Se e são as amplitudes das ondas incidente e refletida, respectivamente, então no caso da reflexão total teremos:
Então:
No limite, o numerador se aproxima de , e o denominador se aproxima de zero, então o valor de tende ao infinito.
Obs.: ROE é a Relação de Ondas Estacionárias, que dá uma razão entre as amplitudes de mínimos e máximos de ondas estacionárias. Mas isso não é tão importante para essa questão.
Passo 2
(b) Para reflexão nula, a amplitude da onda refletida será:
E então:
Passo 3
(c) Agora queremos calcular o seguinte coeficiente de reflexão:
No caso em que . Isso vai exigir algum trabalho algébrico:
Para que a razão aparece na nossa expressão, vamos colocar em evidência no numerador e no denominador:
Agra podemos multiplicar cruzado:
Resposta
(a) .
(b) .
(c) .