Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.Problemas Adicionais - Ex. 99
Uma barra fina, de massa , tem a forma de uma semicircunferência de raio . (a) Qual é a força gravitacional que a barra exerce sobre uma partícula de massa situada no ponto , o centro do arco? (b) Qual seria a força se a barra tivesse a forma de uma circunferência completa?
Passo 1
Temos uma distribuição contínua de massa, então vamos precisar de uma integral para calcular a força gravitacional gerada.
Vamos começar considerando a pequena força gerada por um pequeno pedaço do arco, de massa , que está a uma distância do ponto :
E precisamos encontrar uma expressão para . Se a densidade linear do arco é , então a massa de um trecho de arco é:
E podemos reescrever como :
E podemos calcular a densidade com os dados que foram dados pelo enunciado. Só precisamos dividir a massa pelo comprimento de arco do semicírculo:
Então:
Passo 2
Beleza, já achamos a força gerada por cada pedaço do arco. Agora precisamos integrar para achar a força gerada pelo arco inteiro.
Mas primeiro precisamos usar um argumento de simetria: perceba que para cada pedaço da metade direita do arco, existe um pedaço “espelhado” na metade esquerda, que produz uma força com o mesmo módulo , mas que tem componentes horizontais contrárias:
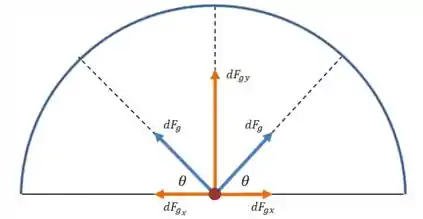
Veja que as componentes se cancelam, e as componentes se somam. Então só precisamos integrar as componentes verticais da força:
Passo 3
(a) Agora é só integrar essa expressão quando varia de até :
A integral de é , então:
Agora é só substituir os valores numéricos:
Passo 4
(b) Se a barra tivesse a forma de uma circunferência completa, o argumento que nós usamos para anular as componentes horizontais no passo , também serviria para anular as componentes verticais.
Em outras palavras, para qualquer pedaço do arco em uma das metades do arco, haveria um outro pedaço com uma componente vertical de mesmo módulo, mas em sentido oposto.
Ou seja, nesse caso a força sobre a partícula seria nula.
Resposta
(a) A força seria de .
(b) Por simetria, a força seria nula.