Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.5 - Ex. 48

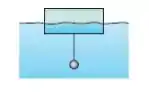
A figura mostra uma bola de ferro suspensa por uma corda de massa desprezível presa em um cilindro que flutua,parcialmente submerso com as bases paralelas à superfície da água. O cilindro tem uma altura de 6   c m ,uma área das bases de 12   c m ² , uma massa específica de 0,30   g / c m 3 e 2   c m de sua altura estão acima da superfície da água. Qual é o raio da bola de ferro?

Passo 1

Belezera galerinha, a figura que o enunciado deu pra gente é essa aqui:

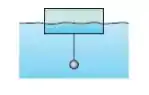
Então seja ρ a densidade do cilindro e ρ F e   a densidade do Ferro. O volume do cilindro nesse caso será:

V = 12   c m 2 × 6   cm

V =   72   cm³  

Passo 2

Iradoso, agora a parte submersa do cilindro tem volume igual a:

V s = 4 × 12   cm³

V s = 48   cm³  

Passo 3

Então dessa maneira, a partir do equilíbrio entre as forças peso e empuxo, obtemos:

ρ g V + ρ F e g V b o l a = V s ρ á g u a g + V b o l a ρ á g u a g

Isolando V b o l a na expressão acima, encontramos:

V b o l a = ρ V - V s ρ á g u a ρ á g u a - ρ F e

Logo:

V b o l a = 3,8   cm³

Como V b o l a = 4 3 π r ³ , temos que:

4 3 π r 3 = 3,8

Isolando r , obtemos:

r = 9,7   mm

Resposta

r = 9,7   mm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um barco que flutua em água doce desloca um volume de água que pesa 35,6k g . (a) Qual é o peso da água que esse barco desloca quando flutua em água salgada de massa especifica 1,10x10 ³k g / m ³ ³ ³?
Uma âncora de ferro de massa específica 7870k g / m ³ ³ parece ser 200N mais leve na água que no ar. (a) qual é o volume da âncora? (b) quanto ela pesa no ar?
Deixa-se cair uma pequena bola a partir do repouso em uma profundidade de 0 , 600m abaixo da superfície em uma piscina com água. Se a massa específica da bola é 0 , 300 vezes a da água e se a força de
Uma esfera de ferro, oca, flutua quase totalmente submersa em água. O diâmetro externo é 60,0c m e a massa específica do ferro é 7,87g / c m ³ ³ . Determine o seu diâmetro interno
Na Fig 14-38, um cubo de aresta L   =   0,600   m e 450   k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030   k g / m ³ ³. Determine (a) o módulo