A figura mostra duas fontes sonoras pontuais isotrópicas, e . As fontes, que emitem ondas em fase, de comprimento de onda , estão separadas por uma distância . Se um detector é deslocado ao longo de uma grande circunferência cujo raio é o ponto médio entre as fontes, em quantos pontos as ondas chegam ao detector (a) exatamente em fase e (b) com fases opostas?

Passo 1
Belezera galerinha, vamos recapitular os pontos principais: o que precisa acontecer para as ondas estarem exatamente em fase?

Mas calma ai que eu te explico meu patrão, a diferença de fase tem que ser um múltiplo inteiro de , tal que:
Com
E para as ondas estarem em fases opostas? A diferença de fase tem que ser um múltiplo ímpar de , tal que.
Com
E vamos lembrar que a fórmula para a diferença de fase é:
Onde é a diferença de percurso das duas ondas até o ponto que estamos analisando.

Passo 2
Belejóia galera, mas agora o enunciado parece ter um erro. Ele fala pra gente em um círculo cujo “raio é o ponto médio entre as fontes”. Mas um raio não é um ponto, é uma distância.

Mas sem pânico galerinha, vamos então considerar que o centro da circunferência é o ponto médio entre as fontes, aí tudo passa a fazer sentido:
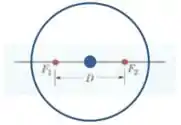
Ok, então pelas fórmulas que acabamos de relembrar, as ondas vão estar “exatamente em fase” nos pontos que atenderem essa relação aqui:
Ou seja:
E vão estar em fases opostas nos pontos que atenderem a essa relação aqui:
Ou seja:
Onde, nos dois casos,

Passo 3
Beleza, agora pense nos pontos da circunferência que estão sobre a reta que liga as fontes.
Bom, em qualquer um desses pontos, a diferença de percurso vai ser (distância entre as fontes). Então:
Opa, isso é simplesmente o caso da fórmula das fases opostas:

Mas como tem dois pontos da circunferência sobre essa reta, vamos dizer dizer que o ponto da esquerda é positivo:
E o da direita é negativo:
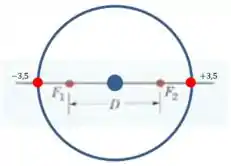
Passo 4
Show de bolinhas, isso já é praticamente a resposta. Como o caso onde os pontos estão sobre a reta que liga as fontes já é o valor máximo da diferença , vai ser o valor máximo que o atinge.
Agora é só contar os pontos!
Por exemplo, vamos percorrer o caminho entre um ponto vermelho e o outro passando pela parte de cima do círculo:
Aí já temos pontos, agora passando pela parte de baixo:
Mais pontos, agora considerando os dois pontos iniciais:
Temos um total de pontos onde as ondas tem fases opostas.
Passo 5
(a) Agora é só usar essa lógica pra achar os pontos com fases iguais. é o valor máximo.
Lembrando que a fórmula era essa aqui:
Quando , a razão fica:
Como são dois pontos opostos, seria: e . Pela mesma explicação do passo 3
E assim como antes vamos ter os seguintes pontos, para e:
Pela parte de cima do círculo:
E pela parte de baixo:
Totalizando pontos em que as ondas estão exatamente em fase.
Passo 6
E o caso da letra (b) já foi até calculado nos passos 3 e 4: também temos pontos onde as ondas tem fases opostas!
Resposta
(a) pontos.
(b) pontos.