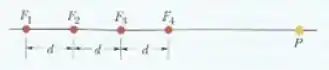
A figura mostra quatro fontes sonoras pontuais isotrópicas uniformemente espaçadas ao longo de um eixo . As fontes emitem sons de mesmo comprimento de onda e mesma amplitude e estão em fase. Um ponto é mostrado sobre o eixo . Suponha que quando as ondas se propagam até a amplitude se mantém praticamente constante. Que múltiplo de corresponde à amplitude da onda resultante em se a distância mostrada na figura é (a) , (b) e (c) ?

Show de bolinhas pessoal, o enunciado nos deu uma figura que mostra quatro fontes sonoras pontuais uniformemente espaçadas ao longo de um eixo . Essas fontes emitem sons de mesmo comprimento de onda e mesma amplitude , além disso elas estão em dase.

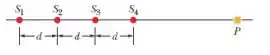
Um ponto é mostrado no eixo . Suponha que quando as ondas se propagam até a amplitude se mantém constante. Sabendo disso, na letra (a), o enunciado quer que a gente encontre qual múltiplo da amplitude corresponde à amplitude da onda resultante em se a distância mostrada na figura é .

Belezoca, o princípio básico da questão é o seguinte: se as ondas estão defasadas por:

Show de bola, então no caso em que , supondo que essa reta onde as fontes estão seja um eixo em que o zero está sobre a fonte , entre as fontes e teremos:

Mas como , vamos obter:

Ou seja, interferência destrutiva!

E agora as fontes e :

Ou seja, exatamente a mesma coisa, desse modo também teremos uma interferência destrutiva.

Ou seja, todas as ondas se cancelam, e a amplitude da onda no ponto é .