Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.3 - Ex. 18
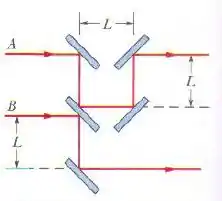
Na figura, as ondas sonoras e , de mesmo comprimento de onda , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda é refletida por quatro superfícies, mas volta a se propagar na direção e no sentido original. O mesmo acontece com a onda , mas depois de ser refletida por apenas duas superfícies. Suponha que a distância da figura é um múltiplo do comprimento de onda . Qual é (a) o menor e (b) o segundo menor valor de para o qual e estão em oposição de fase após as reflexões?
Passo 1
Ok, queremos saber o seguinte. Se aquela distância é algum múltiplo do comprimento de onda:
Qual tem que ser o valor de , para que esse esquema aí da figura faça com que as ondas fiquem em “oposição de fase”? Em outras palavras, que elas fiquem com uma diferença de fase:
Onde
Beleza, antes de tudo vamos lembrar da fórmula que relaciona a diferença de fase com a diferença de percurso :
Lembre: o representa a diferença de distância percorrida pelas ondas!
Agora vamos igualar as duas fórmulas:
Divindo por :
Passo 2
Agora precisamos escrever essa diferença de percurso em função do que está na figura.
Primeiro, qual é a distância percorrida pela onda até seguir em linha reta?
E a onda :
E então:
Mas a questão deu uma fórmula para o :
E substituindo isso na equação de cima:
Passo 3
(a) Beleza, agora queremos saber qual o menor valor que de que gera essa situação. Tranquilo, lembra do que falamos lá em cima?
Então o menor valor de vai ser:
Passo 4
(b) Agora é só seguir a mesma lógica pra achar o segundo menor valor:
Pronto!
Resposta
(a)
(b)