Exercícios de Interferência de Ondas Sonoras - Lista de Exercícios Resolvida
Questão 1
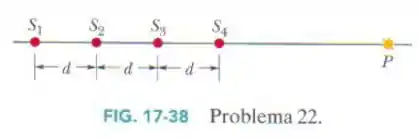
A Fig. 17-38 mostra quatro fontes sonoras pontuais isotrópicas uniformemente espaçadas ao longo de um eixo . As fontes emitem sons de mesmo comprimento de onda e mesma amplitude e estão em fase. Um ponto é mostrado sobre o eixo . Suponha que quando as ondas se propagam até a amplitude se mantém praticamente constante. Que múltiplo de corresponde à amplitude da onda resultante em se a distância mostrada na figura é (a) , (b) , (c) ?
Questão 2
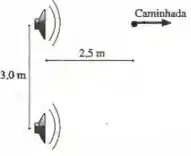
Você está parado diretamente à frente de um dos dois alto-falantes mostrados na figura. Eles estão afastados por de distância e emitem, em fase, um tom de . À medida que você se afasta perpendicularmente ao alto-falante, a que distâncias do alto-falante você escuta um mínimo de intensidade sonora? A temperatura ambiente é .
Questão 3
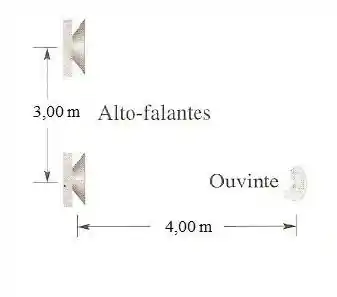
Na figura abaixo dois alto-falantes, separados por uma distância de emitem ondas sonoras em fase. Suponha que as amplitudes do som vindo dos alto-falante são aproximadamente as mesmas na posição de um ouvinte, que está a em linha reta em frente de um dos alto-falantes.
- Para que frequências na faixa de a o ouvinte escutará um sinal máximo?
- Para que frequências nesta faixa ele escutará um sinal mínimo?
Dado:
Ver solução completaQuestão 4
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, , se propagam na mesma direção e no mesmo sentido a . As fontes estão em fase. Qual é a diferença de fase das ondas em um ponto que está a de uma fonte e a da outra?
Ver solução completaQuestão 5
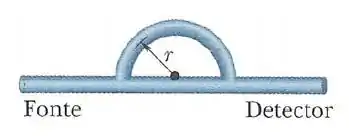
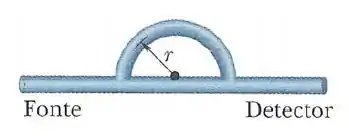
Uma onda sonora com comprimento de onda de propaga-se para a direita num tubo que possui uma bifurcação (vide figura). Ao chegar à bifurcação a onda se divide em duas partes. Uma propaga-se em um tubo em forma de semicircunferência, e a outra se propaga em um tubo retilíneo. As duas ondas combinam-se mais adiante, antes de chegarem ao detector. Qual é o menor raio da semicircunferência para o qual a intensidade medida pelo detector é mínima? Se necessário, use .
Questão 6
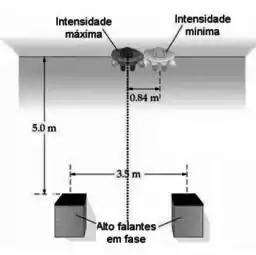
- Dois alto-falantes estão emitindo em fase e estão afastados por uma distância de à frente (ver figura). Um ouvinte encostado na parede ouve um som de máxima intensidade quando se encontra à mesma distância dos alto-falantes. Ao se deslocar ao longo da parede, a intensidade sonora diminui e passa por um mínimo em
- Calcule a frequência do som emitido pelos alto-falantes.
- Suponha que o ouvinte está nessa posição deslocada. Calcule as duas menores frequências que os alto-falantes devem emitir para que seja detectado um máximo de intensidade.
Questão 7
- Na figura abaixo, dois alto-falantes e estão separados por uma distância em um palco ao ar livre. Durante o teste do som, os dois alto-falantes emitem, em fase, sons com comprimento de onda
- Um ouvinte encontra-se inicialmente sobre o eixo a do alto falante e pode se deslocar sobre esse eixo em direção a Considere apenas os valores de .
- Encontre as duas posições do ouvinte em que a intensidade sonora passa por um mínimo (interferência destrutiva).
- Em que posição(ões) do ouvinte a intensidade sonora passa por uma máximo(interferência construtiva)?
Questão 8
(Capítulo 15.Exercícios – Exercícios 29) Suponha que o pulso que se desloca para a esquerda no Exercicio 15.28 esteja abaixo do nivel da corda não esticada, em vez de acima. Desenhe os mesmo diagramas que voce desenhou naquele exercicio.
Ver solução completaQuestão 9
Uma onda sonora com comprimento de onda de propaga-se para a direita num tubo que possui uma bifurcação (vide figura). Ao chegar à bifurcação a onda se divide em duas partes. Uma propaga-se em um tubo em forma de semicircunferência, e a outra se propaga em um tubo retilíneo. As duas ondas combinam-se mais adiante, antes de chegarem ao detector. Qual é o menor raio da semicircunferência para o qual a intensidade medida pelo detector é mínima? Se necessário, use .
Questão 10
Na figura abaixo dois alto-falantes, separados por uma distância de emitem ondas sonoras em fase. Suponha que as amplitudes do som vindo dos alto-falante são aproximadamente as mesmas na posição de um ouvinte, que está a em linha reta em frente de um dos alto-falantes.
- Para que frequências na faixa de a o ouvinte escutará um sinal máximo?
- Para que frequências nesta faixa ele escutará um sinal mínimo?
- Suponha agora que o alto-falante mais distante do ouvinte seja desligado e que o ouvinte comece a andar em direção ao outro alto-falante com velocidade . Se o alto-falante esta emitindo ondas com frequência , que frequência escutará o ouvinte?
Dado:
Ver solução completaQuestão 11
Um alto-falante gera uma onda de . Conforme mostrado na figura, o som se propaga dentro de um tubo que se divide em dois segmentos, um maior que o outro. As ondas sonoras se recombinam, antes de serem detectadas por um microfone. A velocidade do som no ar é de . Qual é a diferença mínima nos comprimentos dos dois caminhos entre os dois segmentos para que as ondas cheguem exatamente fora de fase no microfone?
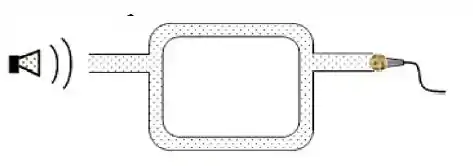
Questão 12
Dois alto-falantes posicionados em um plano estão separados verticalmente por e em fase um com o outro. Ambos emitem ondas sonoras de em um ambiente onde a velocidade do som é . Um ouvinte encontra-se parado à frente dos alto-falantes e a acima da reta que passa pelo ponto médio entre os mesmos. Nesse ponto onde está o ouvinte, a interferência é totalmente construtiva, totalmente destrutiva ou intermediária? Como mudará a situação se os alto-falantes estiverem fora de fase?
- Totalmente Destrutiva; Totalmente Construtiva.
- Totalmente Construtiva; Totalmente Destrutiva.
- Totalmente Destrutiva; Intermediária.
- Intermediária; Totalmente Destrutiva.
- Totalmente Construtiva; Intermediária
Questão 13
Dois alto-falantes idênticos estão voltados um de frente para o outro, separados por 5,00 m de distância. Eles estão em fase, ambos a uma frequência de 875 Hz. A velocidade do som na sala em que os auto-falantes se encontram é de 344 m/s. Uma pessoa está localizada a meio caminho entre os alto-falantes. Ache a distância mais curta que ela pode caminhar em direção a qualquer alto-falante para ouvir um mínimo de som.
A) 0,0983 m
B) 0,197 m
C) 0,295 m
D) 0,393 m
E) 0,590 m
Ver solução completaQuestão 14
Na figura abaixo, temos 2 fontes idênticas emitindo ondas circulares no plano. No ponto C da figura, a interferência é:
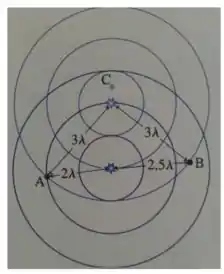
- Totalmente construtiva.
- Parcialmente construtiva.
- Totalmente destrutiva.
- Parcialmente destrutiva.
- Não há interferência no ponto C.
Questão 15
Três alto-falantes , e emitem ondas sonoras idênticas e em fase. Os alto-falantes estão em posições diferentes em relação ao detector , mas todos estão contidos em um mesmo plano, como ilustrado na figura ao lado.
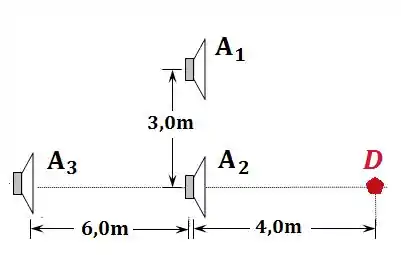
- Suponha que o alto-falante está desligado, ou seja, considere apenas os alto-falantes e . Nesse caso, quais são os comprimentos de onda que fazem com que nenhum sinal sonoro chegue ao detector ?
- Agora, suponha que o alto-falante foi ligado, de forma que os três alto-falantes estão emitindo ondas sonoras. Nesse caso, qual é a menor frequência que faz com que o som que chegue ao detector tenha a maior amplitude possível?
Dados:
Ver solução completaQuestão 16
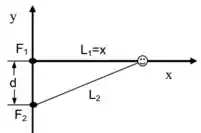
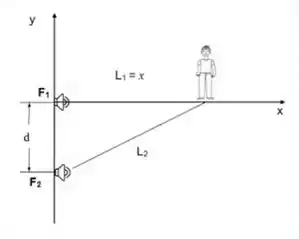
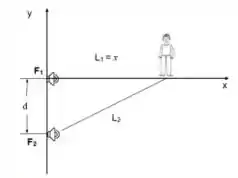
Uma fonte de som A está na posição e outra fonte B em . As duas fontes emitem coerentemente e em fase. Um observador encontra-se no ponto . Qual é a menor frequência que faz com que a intensidade sonora medida pelo observador seja mínima? Suponha que a velocidade do som é
Ver solução completaQuestão 17
I. Considere uma fonte sonora F e um detector D, posicionados conforme a figura. Admita que D receba o som de F pelos caminhos 1 (direito) e 2 (com reflexão). Considere que na reflexão há uma mudança de fase de .
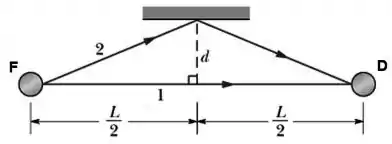
Sendo L= 8,00 m, 85 Hz a frequência das ondas e 340m/s a velocidade do som, obtenha o menor valor de d (diferente de zero) para que ocorra no detector:
a) interferência construtiva;
b) interferência destrutiva;
Ver solução completaQuestão 18
Dois alto-falantes A e B estão a uma distância de 300 m e 400 m, respectivamente, de um ouvinte. Suponha que as ondas sonoras que saem dos alto-falantes possuem frequencias, fases e amplitudes iguais quando emitidas. Considerando que a faixa de frequência audível de um ser humano normal vai de 20 Hz a 20 kHz, qual é a menor frequência para a qual a intensidade do som é máxima na posição do ouvinte?
Considere a velocidade do som .
a) 21 Hz b) 25 Hz c) 35 Hz d) 40,5 Hz e) 200 Hz f) 240 Hz g) 400 Hz h) 440 Hz i) 480 Hz.
Ver solução completaQuestão 19
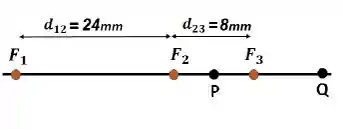
A figura ao lado mostra três fontes sonoras pontuais (F1,F2 e F3). As fontes emitem sons idênticos simultaneamente, em todas as direções, com comprimento de onda λ = 16 mm e amplitude Sm = 1 mm. Considere que a distância entre as fontes 1 e 2, e a distância entre as fontes 2 e 3 são iguais a d12 = 24 mm e d23 = 8 mm respectivamente. Dois pontos P e Q são mostrados na figura. Considere que o ponto P se encontra equidistante às fontes 2 e 3. Marque a alternativa que corresponde às amplitudes da onda resultante em P e Q respectivamente:
a)
b)
c)
d)
e)
f)
g)
h)
i)
Ver solução completaQuestão 20
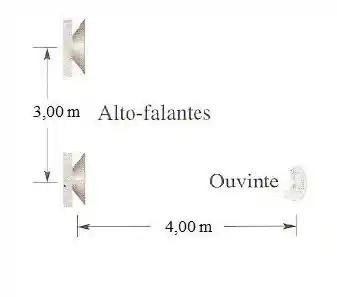
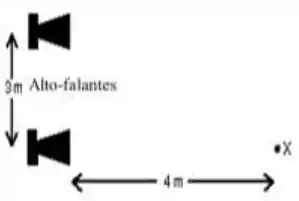
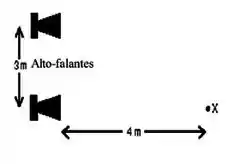
Dois pequenos alto-falantes são ligados (em fase) à mesma fonte de sinal. Os alto-falantes estão separados por uma distância de 3,0 m. Um observador se encontra no ponto X, com o ouvido na mesma altura dos alto-falantes e em frente de um deles, a uma distância de 4,0 m, como mostra a figura. Se os sons emitidos pelos alto-falantes têm a mesma amplitude, a
intensidade do som ouvido pelo observador é a menor possível quando o comprimento de onda é:
- 1 m
- 2 m
- 3 m
- 4 m
- 5 m
Questão 21
Uma corda de comprimento presa nas duas extremidades produz uma onda estacionária descrita pela expressão:
onde e estão em metros e em segundos. A corda possui uma massa de 500 gramas. Considere a fundamental como o primeiro harmônico. Se a corda vibra em seu quinto harmônico, calcule:
- o comprimento da corda;
- a frequência de vibração das ondas na corda;
- a tensão na corda.
- o harmônico produzido no tubo.
Considere agora que a corda vibra nas proximidades de um tubo de comprimento aberto em apenas uma das extremidades. A vibração da corda gera ondas dentro do tubo, que oscilam na mesma frequência de vibração das ondas produzidas na corda. Sob essas circunstâncias, determine:
Dado: velocidade do som no ar = .
Ver solução completaQuestão 22
A função que representa o resultado da interferência de duas ondas transversais, cujas funções de onda são
Questão 23
Dois alto-falantes A e B estão localizados no eixo como mostra a figura abaixo. Eles estão separados por uma distancia de . Cada alto-falante emite ondas sonoras em sentidos opostos, A no sentido e B no sentido , com frequências iguais a , e as fontes estão fora de fase em . A velocidade do som e . A que distancia do alto-falante A ocorrerá o primeiro ponto de interferência construtiva?
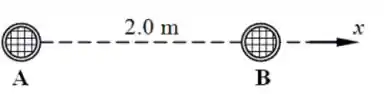
Questão 24
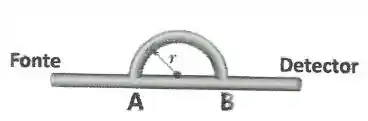
Um som de comprimento de onda λ e frequência ω se propaga para a direita a partir de uma fonte e através de um tubo que, a partir do ponto A, é formado por uma porção reta e uma semicírculode raio r. Parte da onda sonora se propaga em linha reta até o detector (ver figura). O resultado da superposição do som produz uma interferência. Dê suas respostas em termos de π.
a) Calcule a diferença de fase entre as duas frentes de onda no ponto B.
b) Calcule o menor valor de r que resulta em uma intensidade de som mínima no detector.
c) Calcule o menor valor de r que resulta em uma intensidade de som máxima no detector.
Ver solução completaQuestão 25
Dois alto-falantes sobre o eixo emitem ondas sonoras de mesma frequência e comprimento de onda no mesmo sentido ao longo do eixo . A amplitude de cada onda é . A intensidade sonora é mínima quando o alto-falante 2 encontra-se atrás do alto-falante 1. A intensidade aumenta à medida que o alto-falante 2 é movido para a frente e atinge um valor máximo, pela primeira vez, de amplitude , quando se encontra à frente do alto-falante 1. Qual é a amplitude do som, como múltiplo de , se os alto-falantes forem colocados lado a lado?
A)
B)
C)
D)
E)
Ver solução completaQuestão 26
Parte
Na figura abaixo, dois alto-falantes e estão separados por uma distância em um palco ao ar livre. Durante o teste de som, os dois alto-falantes emitem, em fase, sons com comprimento de onda de . Um ouvinte encontra-se inicialmente sobre o eixo a do alto-falante e desloca-se sobre esse eixo em direção a . Considere apenas os valores . Encontre a primeira posição do ouvinte em que a intensidade sonora passa por um mínimo (interferência destrutiva)?
Questão 27
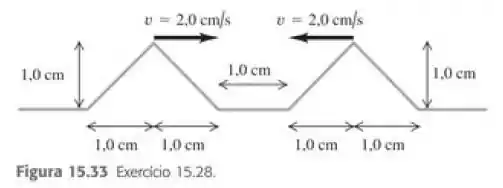
(Capítulo 15.Exercícios – Exercícios 28) Dois pulsos ondulatórios triangulares estão se aproximando em uma corda esticada, como indicado na Figura 15.33. Os dois pulsos são idênticos e se deslocam com velocidade igual a 2,0 cm/s. A distancia entre as extremidades dianteira dos pulsos é igual a 1,0 cm para . Desenhe a forma da corda para
Questão 28
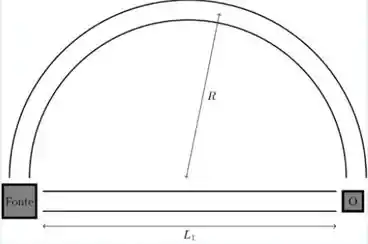
. Uma onda sonora com frequência é emitida de uma fonte posicionada como mostra a figura. A velocidade do som no meio é . O observador, também posicionado na figura, detecta uma onda sonora proveniente da interferência entre as ondas sonoras provenientes da fonte que realizam os diferentes caminhos marcados. Encontre qual a diferença de fase que o observador mede dado que e .
.
.
.
.
.
Ver solução completaQuestão 29
Dois alto-falantes transmitem o mesmo sinal harmônico, recebido em fase de um único oscilador. Os alto-falantes estão a uma distância de 6 m e 8 m, respectivamente, de um microfone que capta o som de ambos. Qual o menor comprimento de onda necessário para que haja interferência (i) completamente construtiva e (ii) completamente destrutiva?
(a) (i) 4 m e (ii) 2 m
(b) (i) 2 m e (ii) 8 m
(c) (i) 2 m e (ii) 4 m
(d) (i) 4 m e (ii) 1 m
(e) (i) 4 m e (ii) 2 m
Ver solução completaQuestão 30
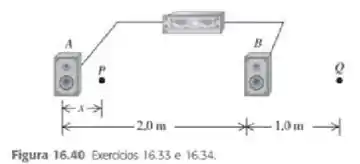
(Cap.16.6 – Ex. 33) Dois alto-falantes, A e B (Figura 16.40), são alimentados por um mesmo amplificador e emitem ondas senoidais em fase. O alto-falante B está a uma distância de à direita do alto-falante A. a velocidade do som no ar é igual a . Considere o ponto Q ao longo da extensão da linha reta que une os dois alto-falantes, situado a uma distância de à direita do alto-falante B. Os dois alto-falantes emitem ondas sonoras que se propagam diretamente dos alto-falantes até o ponto Q. a) Qual é a menor frequência capaz de produzir interferência construtiva no ponto Q? b) Qual é a menor frequência capaz de produzir interferência destrutiva no ponto Q?
Questão 31
Dois pequenos alto-falantes são ligados (em fase) à mesma fonte de sinal. Os alto-falantes estão separados por uma distância de 3,0 m. Um observador se encontra no ponto X, com o ouvido na mesma altura dos alto-falantes e em frente de um deles, a uma distância de 4,0 m, como mostra a figura. Se os sons emitidos pelos alto-falantes têm a mesma amplitude, a intensidade do som ouvido pelo observador é a maior possível quando o comprimento de onda é:
a) 1 m;
b) 2 m;
c) 3 m;
d) 0,75 m;
e) 4 m;
Ver solução completaQuestão 32
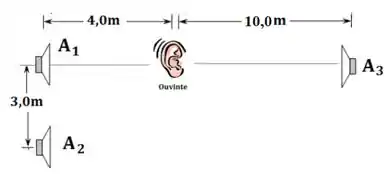
Três alto-falantes e emitem ondas sonoras idênticas e em fase. Os alto-falantes estão em posições diferentes em relação ao ouvinte, mas todos estão contidos em um mesmo plano, como ilustrado na figura. Considere toda faixa de audição de um ser humano médio, , e velocidade do som no ar igual a .
- Suponha que o alto-falante está desligado, ou seja, considere apenas os alto-falantes . Nesse caso, quais são os comprimentos de onda que fazem com que nenhum sinal sonoro seja detectado pelo ouvinte?
- Ainda nesse caso, quantas possíveis frequências existem na faixa de audição do ser humano médio?
- Agora, suponha que o alto-falante foi ligado, de forma que os três alto-falantes estão emitindo ondas sonoras. Nesse caso, qual é a menor frequência que faz com que o som que chegue ao ouvinte tenha a maior amplitude possível?
Questão 33
Dois alto-falantes idênticos, separados por uma distância , emitem ondas sonoras de frequência e intensidade em direções opostas, conforme mostra a figura abaixo. Considerando a velocidade do som e supondo que a intensidade de cada alto-falante é constante na região entre eles, podemos afirmar que as intensidades do som respectivas aos pontos A, B e C, indicados na figura são:

a)
b)
c) ;
d) ;
e) ;
f ) .
Ver solução completaQuestão 34
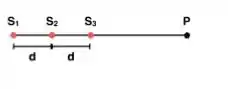
A figura ao lado mostra três fontes sonoras pontuais isotrópicas uniformemente separadas ao longo de um eixo . As fontes emitem sons de mesmo comprimento de onda λ, mesma amplitude e estão em fase. Um ponto é mostrado sobre o eixo . Suponha que quando as ondas se propagam até suas amplitudes se mantêm praticamente constantes. Qual é a amplitude de onda resultante em se a distância mostrada na figura for, respectivamente, λ/4, λ/2 e λ?

Questão 35
Duas ondas senoidais de mesma amplitude se superpõem e sofrem interferência. Em quatro pontos diferentes do espaço as diferenças de fase entre as ondas são de radianos. Qual é o ordenamento correto em função das amplitudes da onda resultante, começando pela maior?
Questão 36
Na figura abaixo, dois alto-falatntes e estão separados por uma distância em um palco ao ar livre. Durante o teste de som, os dois alto-falantes emite, em fase, sons com comprimento de onda de . Um ouvinte encontra-se inicialmente sobre o eixo a do alto-falante e desloca-se sobre esse eixo em direção a . Considere apenas os valores . Encontre a primeira posição do ouvinte em que a intensidade sonora passa por um mínimo (interferência destrutiva)?
 Escolha uma:
Escolha uma:
- Nenhuma das alternativas